The Effective Interest Rate reflects the true annual yield or cost of an investment or loan gainable or payable due to the compounding over the period.
Effective Interest Rate – an Example
The effective interest rate is the interest rate that you get or have to pay on your investment or for your loan. For a given interest rate and frequency of compounding within a year:
= (1 + i/n)n – 1The offered Interest Rate = i
And Frequency of the Compounding in a Year = n
You took a loan of $10,000 from a local bank with an annual percentage rate of 12%.
The interest will be compounded every month:
Annual Percentage Rate/Nominal Interest Rate: 12%
The monthly interest rate: 12%/12 = 1%
At the end of Month 1: your Principal + Interest will be: $10,000 + $10,000 x 1% = $10,000 (1 + 0.01) = $10100
If you did not pay the interest ($100) for the first month, in the 2nd month your principal will be $10,100.
At the end of Month 2: your Principal + Interest will be = $10100 + $10100 x 1% = $10201
To create a formula from the above statement:
= $10100 + $10100 x 1%
= $10100 (1 + 1%)
= $10,000 x (1 + 1%) x (1 + 1%); As $10100 = $10,000 x (1 + 1%)
= $10,000 x (1 + 1%) ^2; As (1 + 1%) x (1 + 1%) = (1 + 1%) ^2
= $10,000 x (1 + 0.01) ^ 2
At the end of the 3rd month, your Principal + Interest will be: $10,000 x (1 + 0.01) ^ 3
… … …
… … …
… … …
After 12 months, your Principal and Interest will be: $10,000 x (1 + 0.01) ^12 = $11268.25
You are going to pay a total interest: ($11268.25 – $10,000) / $10,000 = 12.68%.
The bank indicated an Annual Percentage Rate of 12%.
That is the Nominal Interest Rate, but due to compound interest monthly, you’re paying more than the nominal interest rate.
Method 1 – Using the IRR Function to Calculate the Effective Interest Rate On Discount Bonds
The syntax of the IRR function is
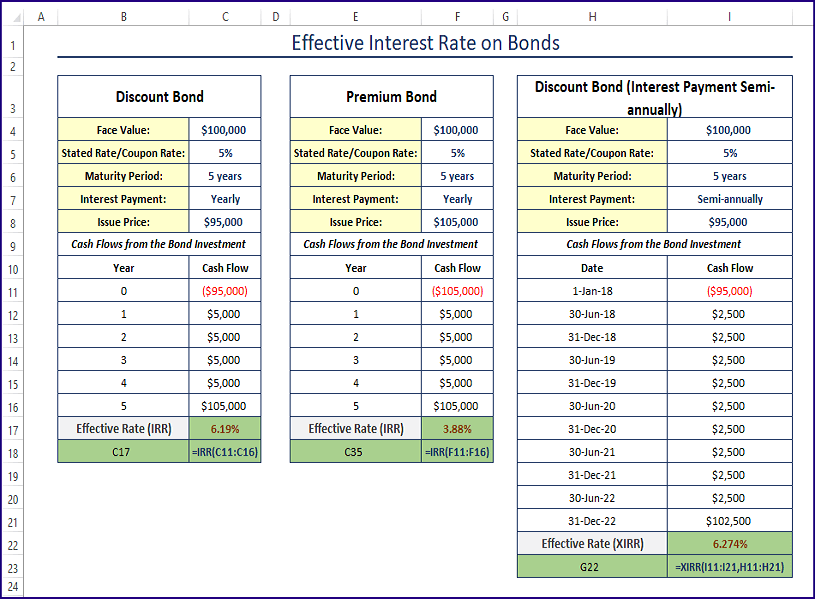
IRR (values, [guess])The details of the discount bond are depicted in the image below.

Steps:
- Enter the following formula in C17.
=IRR(C11:C16)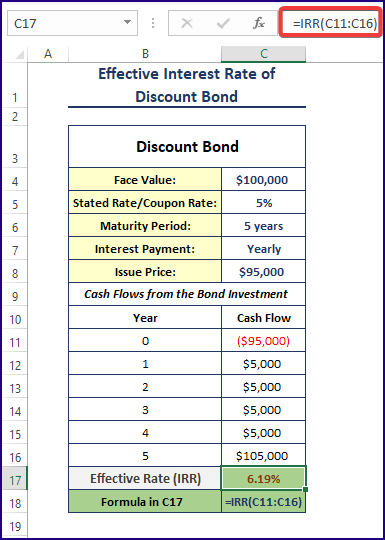
Formula Breakdown
- In year 0, you invest $95,000 (the issue price of the bond) to buy the bond. You pay $95,000 because it’s a discount bond.
- At the end of the 1st year, you get $5,000 as the interest payment from the bond issuer. The face value of the bond is $100,000 and the nominal yearly interest rate is 5%. You get an interest payment amount of: $100,000 x 5% = $100,000 x 0.05 = $5,000.
- After the 2nd, 3rd, and 4th years, you get interest payments of $5,000.
- At the end of the 5th year, you get $105,000. Because your bond has matured. You get back the face value of the bond, of $100,000 + the yearly interest of $5,000 = $105,000.
- The IRR (Internal Rate of Return) or the Effective Interest Rate was calculated in C17: =IRR (C11: C16)
Method 2 – Calculating the Effective Interest Rate for Premium Bonds in Excel
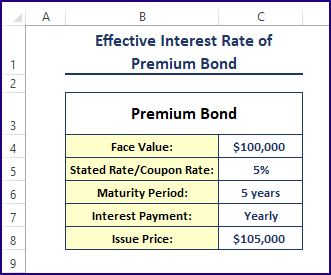
The basic components of the premium bond are shown below.
Steps:
- Use the formula in any blank cell (here, C17).
=IRR(C11:C16)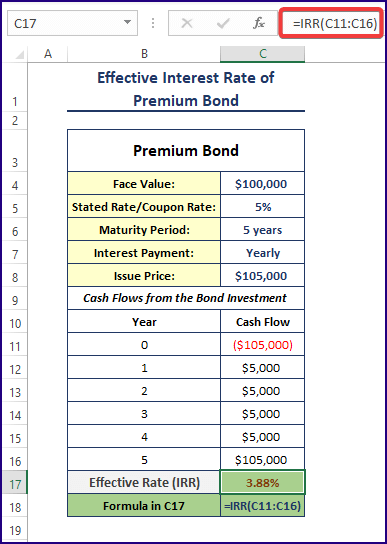
Formula Breakdown
- The issue price is $105,000. In year 0, the investment is -$105,000.
- After years 1, 2, 3, and 4, the bondholder will get $5,000 in interest payments. The bond’s face value is $100,000 and its yearly nominal interest rate is 5%. The yearly interest payment is $100,000 x 5% = $5,000.
- At the end of year 5, the bond will mature. The bondholder will get the face value amount and the yearly interest payment: $100,000 + $5,000 = $105,000.
- The IRR function was used to calculate the internal rate of return or effective interest rate for these cash flows in C17: =IRR (C11: C16).
Method 3 – Finding the Effective Interest Rate for Semi-annually Payments
The syntax of the XIRR function is
XIRR (values, dates, [guess])The fundamental components of the discount bond are shown below.

Steps:
- Use the following formula in C22.
=XIRR(C11:C21,B11:B21)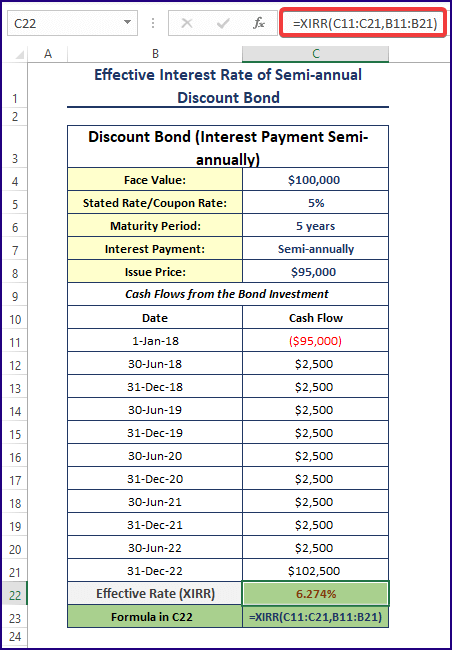
Formula Breakdown
- As the interest payments are done semi-annually (twice a year), the stated rate/nominal interest rate of 5% is divided by 2: 2.5%. The semi-annual interest payment will be $100,000 x 2.5% = $2,500.
- When the bond matures, you will get $102,500 (face value + the last 6 months’ interest). To get the internal rate of return or the effective rate of these cash flows, use Excel’s XIRR function.
- C11: C21 are the cash flows received, and B11: B21 is the date of receiving the cash flows. 6.274% is the effective interest rate for these cash flows.
Read More: How to Perform Interest Rate Swap Calculation in Excel
Method 4 – Applying the EFFECT Function to Calculate Different Effective Interest Rates
The syntax of the EFFECT function is:
EFFECT(rate,periods)Steps:
- Use the following formula to calculate the effective interest rates for a given interest rate and frequencies.
=EFFECT($E$3,C6)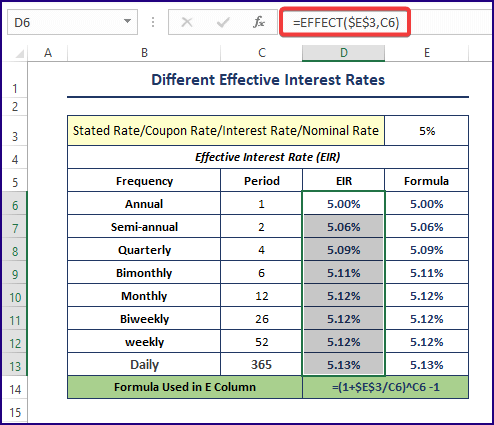
Use the typical Effective Interest Rate formula ( (1 + i/n)n – 1) in the adjacent cell to cross-check the output of the EFFECT function.
Download Excel Workbook
Related Articles
- Create Flat and Reducing Rate of Interest Calculator in Excel
- How to Perform Interest Rate Sensitivity Analysis in Excel
<< Go Back to Interest Rate Calculator | Finance Template | Excel Templates
Get FREE Advanced Excel Exercises with Solutions!


I want printed materials for courses
You can copy the article and paste in a word file and then use it personally. Thanks.