Example 1 – Solving the Traveling Salesman Sequencing Problem Using the Solver
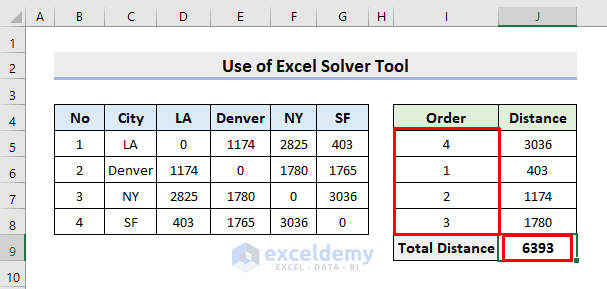
The sample dataset contains 4 Cities and the Distance between them. We’ll find out a sequence of the cities for a traveling salesman so that the total distance covered will be minimal.
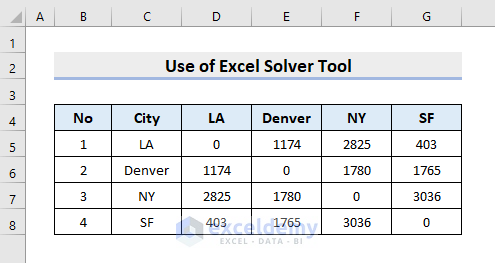
STEPS:
- We’ll set up a random order in the I column as shown below.
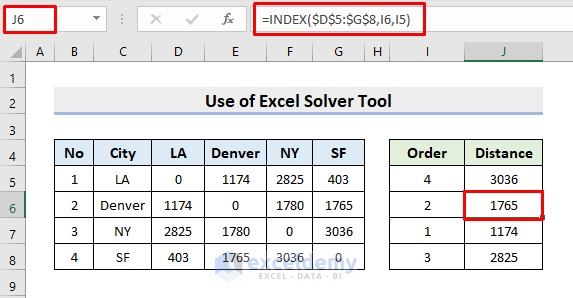
- Select cell J6.
- Insert the formula:
=INDEX($D$5:$G$8,I6,I5)- Press Enter. The INDEX function extracts the distance between the cities specified in I6 and I5.
- Use AutoFill to get the other outputs.
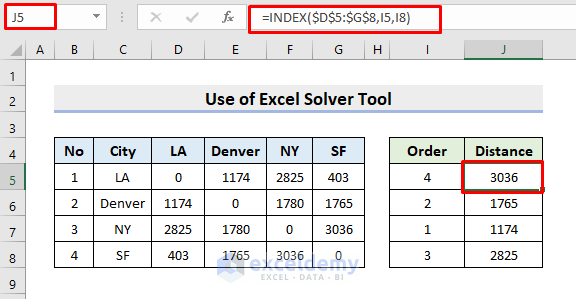
- Select cell J5.
- Input the formula:
=INDEX($D$5:$G$8,I5,I8)- Click Enter.
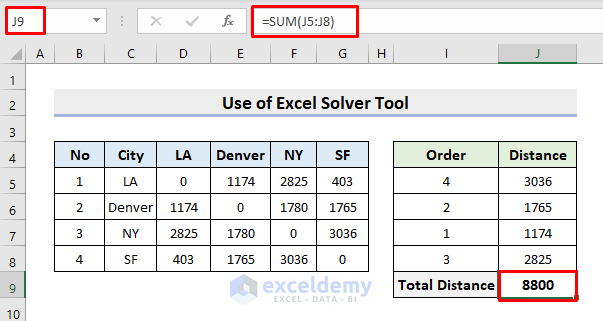
- Use the AutoSum feature in cell J9 to calculate the total distance.
- Go to File and select Options.
- The Excel Options box will pop out.
- In the Add-ins tab, select Excel Add-ins and choose Go.
- Check the box for Solver Add-in.
- Press OK.
- Click Data and select Solver.
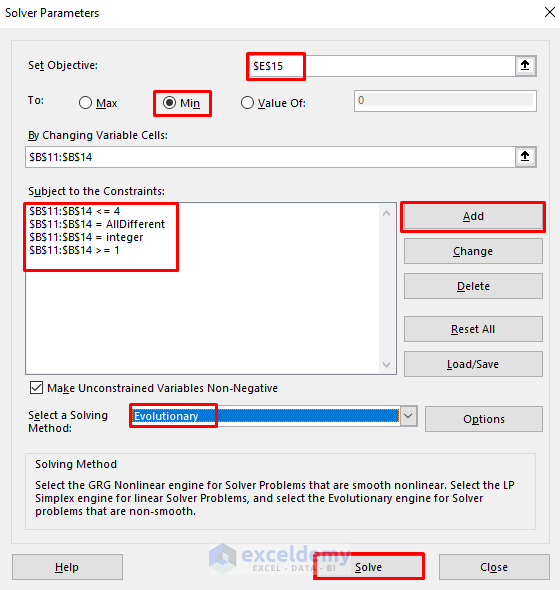
- In the Solver Parameters dialog box, select Set Objective and put E15.
- Choose Min.
- Select B11:B14 from the data for the By Changing Variable Cells
- We’ll add the constraints by clicking the Add button.
- Our constraints are:
B11:B14 <= 4
B11:B14 = AllDifferent
B11:B14 = integer
B11:B14 >= 1
- Select Evolutionary as the solving method.
- Press Solve.
- This’ll return a new sequence where the total distance is the lowest value possible.
- In this way, we can solve sequencing problems using the Solver tool.
Read More: How to Use Excel Solver for Linear Programming
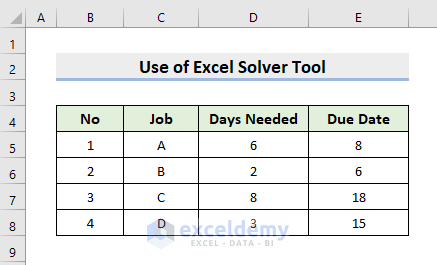
Example 2 – Apply the Solver to Solve the Job Schedule Sequencing Problem
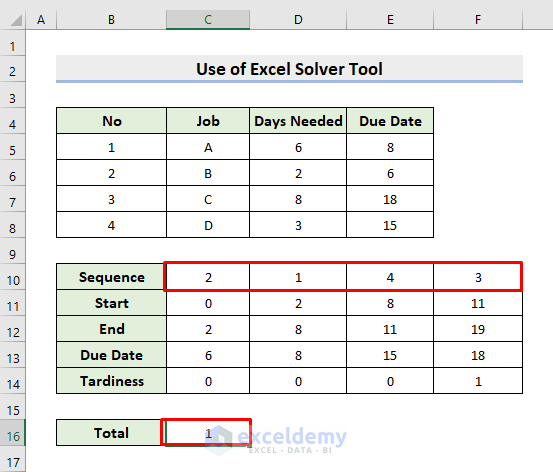
The following dataset has 4 types of Jobs, Days Needed, and Due Dates. We’ll make an order of the jobs where the Tardiness will be as little as possible.
STEPS:
- Create a random sequence.
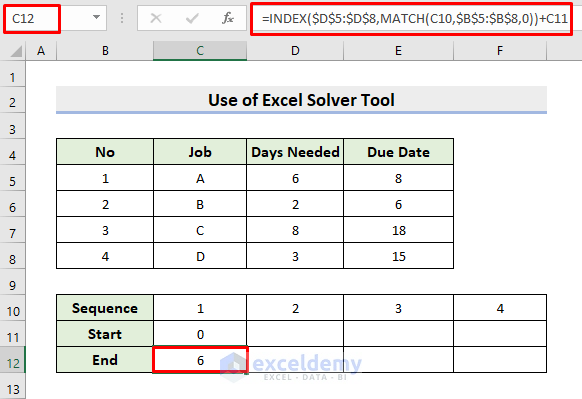
- As a starting day, 0 is placed in cell C11.
- Select cell C12.
- Insert the formula:
=INDEX($D$5:$D$8,MATCH(C10,$B$5:$B$8,0))+C11- Press Enter to get the result. The MATCH function looks for the C10 cell value in the range B5:B8 and returns the position. The INDEX function extracts the days needed to complete the specified task.
- The starting date is added to the function output to get the finishing date.
- Select cell D11 and input the formula:
=C12- Press Enter to get the starting date of the next task.
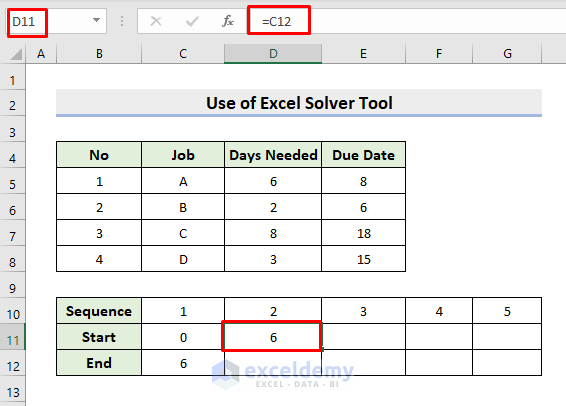
- Use AutoFill to complete the starting and ending series.
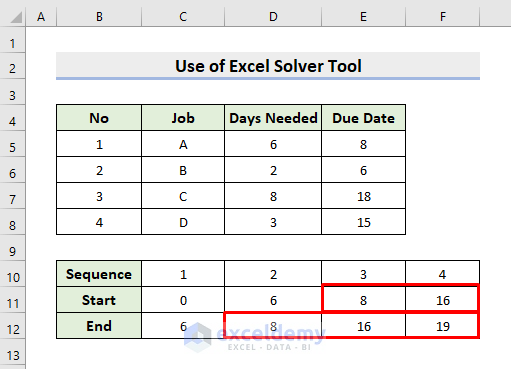
- Choose cell C13 to insert the formula:
=INDEX($E$5:$E$8,MATCH(C10,$B$5:$B$8,0))The MATCH function extracts the position of a specific task. The INDEX function returns the due date for that task.
- Apply AutoFill.
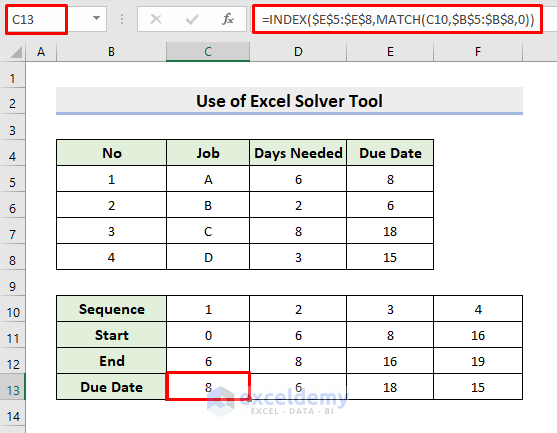
- Select cell C14.
- Input the formula:
=MAX(0,C12-C13)- Click Enter. The MAX function compares the values and returns the largest.
- Use AutoFill.
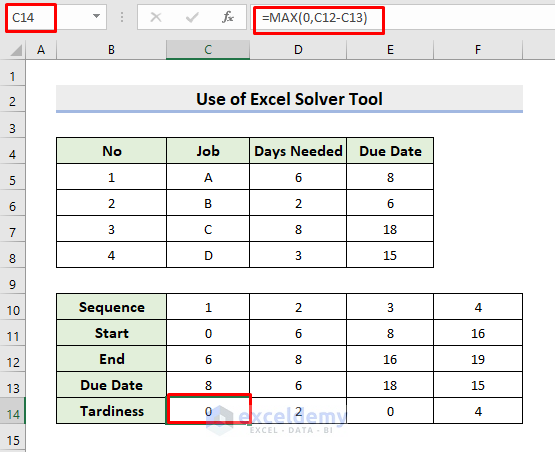
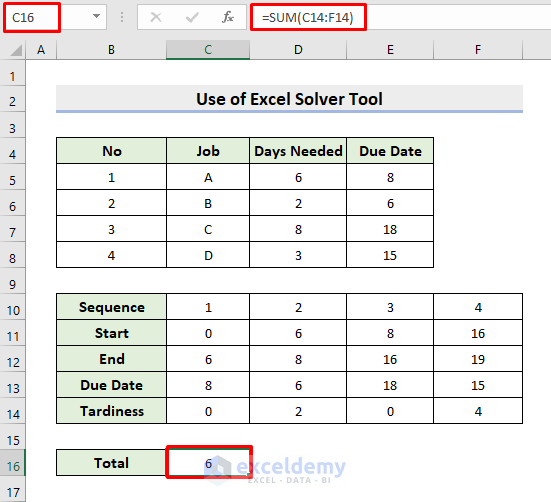
- To calculate the total tardiness, click cell C16 and insert:
=SUM(C14:F14)- Press Enter.
- Go to Data and select Solver. To enable it, see the process in Example 1.
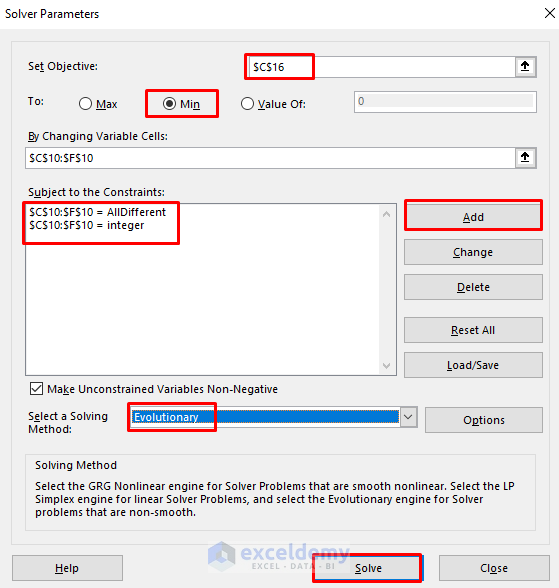
- In the pop-out dialog box, set C16 as the objective.
- Choose Min.
- We’ll change C10:F10 as the variables.
- The constraints in this problem are:
C10:F10 = AllDifferent
C10:F10 = integer
- Choose Evolutionary as the solving method.
- Click Solve.
- You’ll get the best sequence with as little as possible tardiness.
Read More: Example with Excel Solver to Minimize Cost
Download the Practice Workbook
Related Articles
- How to Use Excel Solver to Rate Sports Team
- How to Use Excel Solver to Determine Which Projects Should Be Undertaken?
- Solving Transportation or Distribution Problems Using Excel Solver
- How to Assign Work Using Evolutionary Solver in Excel
- Resource Allocation in Excel
- Solving Equations in Excel
- How to Do Portfolio Optimization Using Excel Solver
<< Go Back to Excel Solver Examples | Solver in Excel | Learn Excel
Get FREE Advanced Excel Exercises with Solutions!


Thank you Professor for the nice and useful illustration. I teach subjects like Operations Management ad Decision Science and use Excel for solving the problems. Your methods are very helpful. Can you kindly explain how to solve sequencing problem using Johnson’s algorithm of scheduling n-jobs on 2-machines?
Greetings, Raja.
I appreciate you asking this question. You can find it here “Sequencing problem using Johnson’s algorithm of scheduling n-jobs on 2-machines”
I will pass your request to the author, Jagadeesh!
Glad to know it helped you!
Thank you for the very informative tutorial.
I would like some advice though to take the shop scheduling problem 1 step further.
How can I do this at a time/hour level – rather than day?
For example – if we have x amount of jobs in queue; varying in duration
We can only turn around jobs during standard work hours (7 AM and 4 PM).
We also need to meet delivery dates.
How do I arrange jobs in a way that maximizes machine utilization?
Greetings, LOIACONO.
I appreciate you asking this question. You have to follow the “3 Shop Scheduling Problem” example from this article. If you wish to do the calculation at a time/hour level instead of a day level, you need to input hours instead of days in the Days needed column. You must then follow the example’s rest of the process to arrange jobs in a way that maximizes machine utilization.
Nice model that can be simplified a bit because the help file for solver stats that:
“A constraint such as A1:A5 = alldifferent, where A1:A5 are decision variable cells, requires that these cells must be integers in the range 1 to N (N = 5 in this example), with each variable different from all the others at the solution.”
So constraints G3:G8=1 and G3:G8 = integer are not needed
Alf
Greetings, ALF.
It was helpful to receive the information you provided.