How to Calculate Levenshtein Distance in Excel (4 Easy Methods)

The Levenshtein Distance, also known as the Edit distance, is named after Soviet mathematician Vladimir Levenshtein, who in 1965 first shared the thought about the distance between two words. This distance tells us how many edits need to be done to make two strings the same.

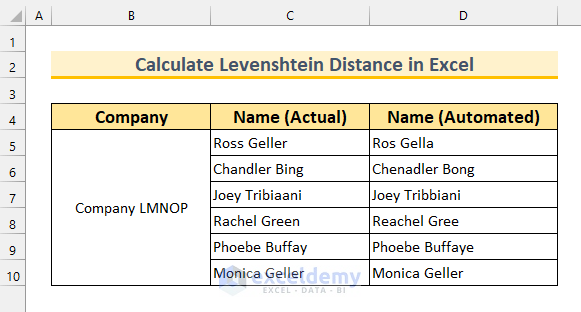
For example, making “Ross Geller” and “Ros Gella” the same requires the following edits:

First, we need to add an “s”.
Next, we need to replace “a” with “e”.
Finally, “r” is added to make both words the same.

Thus the Levenshtein distance between those two words is 3. Similarly, “Apex” and “Apox” will have 1 Levenshtein distance between them (changing “e” or “o”).

In this article, we will show you 4 methods of how to calculate Levenshtein distance in Excel. To demonstrate our methods, we have selected a dataset with 3 columns: “Company”, “Name (Actual)”, and “Name (Automated)”, which represents employee names collected through 2 methods. Let’s find the distance between these two.

Method 1 – Using a Custom Function

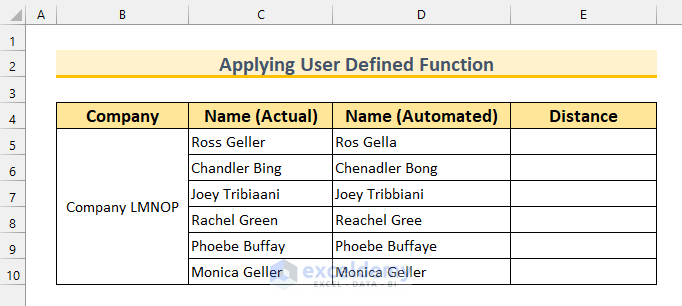
We can create a User Defined function inside the VBA Module to calculate Levenshtein distance in Excel. To illustrate, we have added a new column “Distance” to our dataset.

Steps:

To open the VBA Module, from the Developer tab select Visual Basic.
Alternatively, you can press ALT+F11.

The “Microsoft Visual Basic for Application” will appear.

From Insert, select Module.

Enter the following code inside the Module:

Option Explicit
Public Function Levenshtein_Distance(x1 As String, x2 As String)
Dim p As Integer
Dim q As Integer
Dim r As Integer
Dim s As Integer
Dim lDistance() As Integer
Dim t As Integer
Dim u As Integer
r = Len(x1)
s = Len(x2)
ReDim lDistance(r, s)
For p = 0 To r
    lDistance(p, 0) = p
Next
For q = 0 To s
    lDistance(0, q) = q
Next
For p = 1 To r
    For q = 1 To s
        If Mid(x1, p, 1) = Mid(x2, q, 1) Then
            lDistance(p, q) = lDistance(p - 1, q - 1)
        Else
            t = lDistance(p - 1, q) + 1
            u = lDistance(p, q - 1) + 1
            If u < t Then
                t = u
            End If
            u = lDistance(p - 1, q - 1) + 1
            If u < t Then
                t = u
            End If
            lDistance(p, q) = t
        End If
    Next
Next
Levenshtein_Distance = lDistance(r, s)
End Function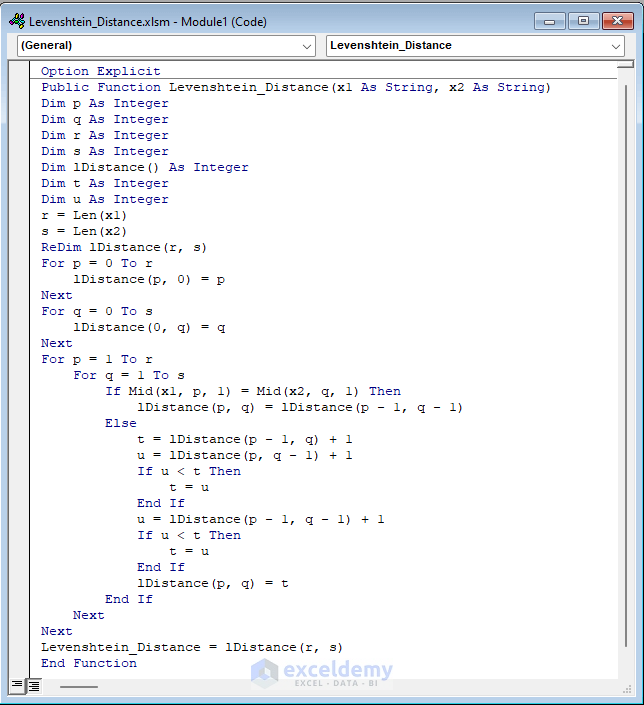

VBA Code Breakdown

We call our Function Levenshtein_Distance.
We define the variable types.
We find the string lengths of two values, which we will provide inside the function.
We use the For Next Loop to go through our all alphabets.
Thus, we can find our target distance; we just need to run this function inside our dataset.

Select cell E5 and enter the following formula:

=Levenshtein_Distance(C5,D5)

We provide the two strings in cells C5 and D5 to find the distance between them.

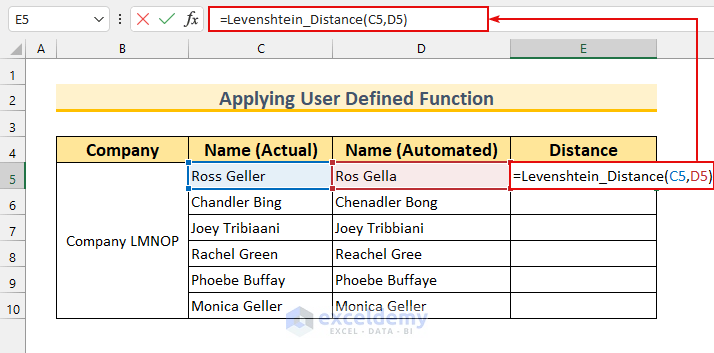
Press ENTER and AutoFill the formula to the rest of the cells.

The output should look like this.

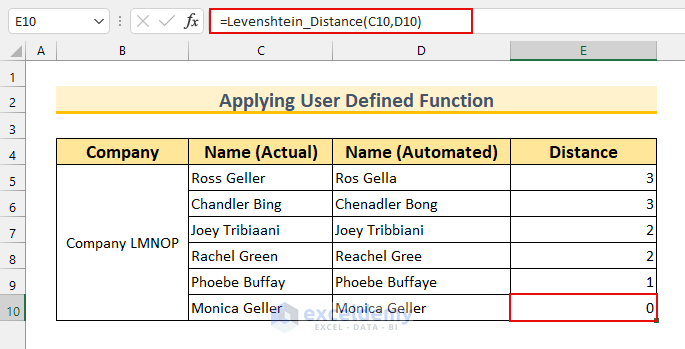
Method 2 – Creating a Matrix

We can create a Matrix to find out the Levenshtein distance between two strings. To demonstrate, we have added a few cells to our dataset. Moreover, we use MID, IF, OR, LEN, MIN, and OFFSET functions here.

We will calculate the distance between “Exceldemy” and “Microsoft”. There are 12 rows and columns in the Matrix, but you can add as many as you need.

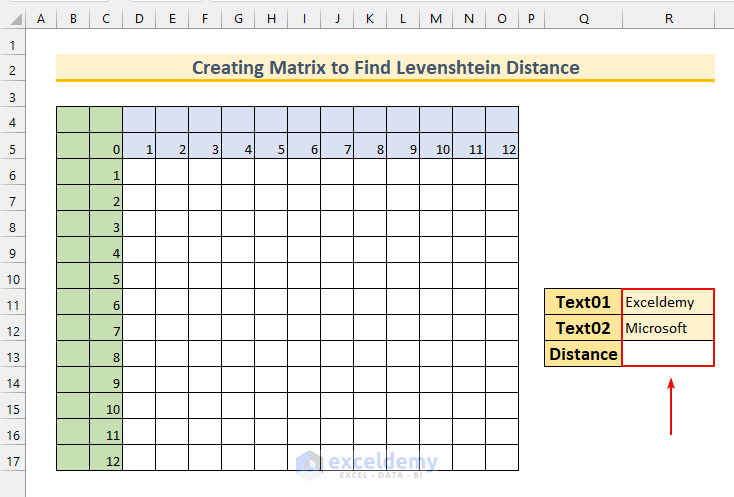
Steps:

Select the cell range D4:O4.
Enter the following formula:

=MID($R$11,D5,1)

The MID function returns a number of characters from a value. Here, the value of cell D5 is 1. Therefore, we are telling the function to return the first character from the “Exceldemy” string. Hence, we will get “E” as the output.

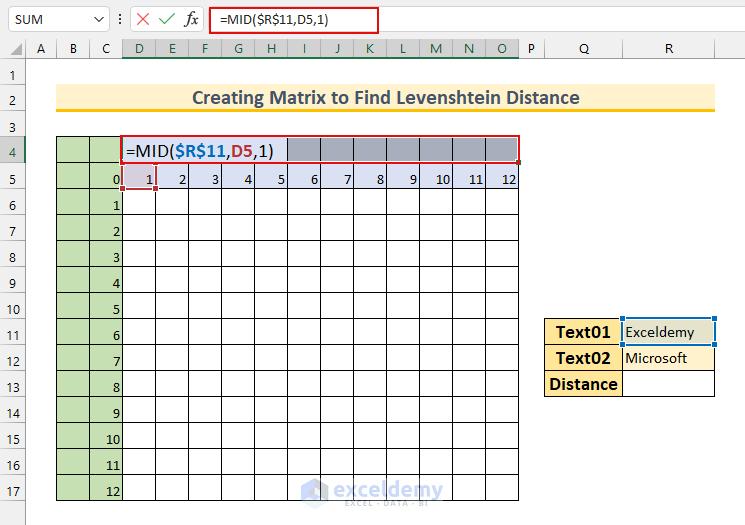
Press CTRL+ENTER, which will AutoFill our formula to the selected cells.

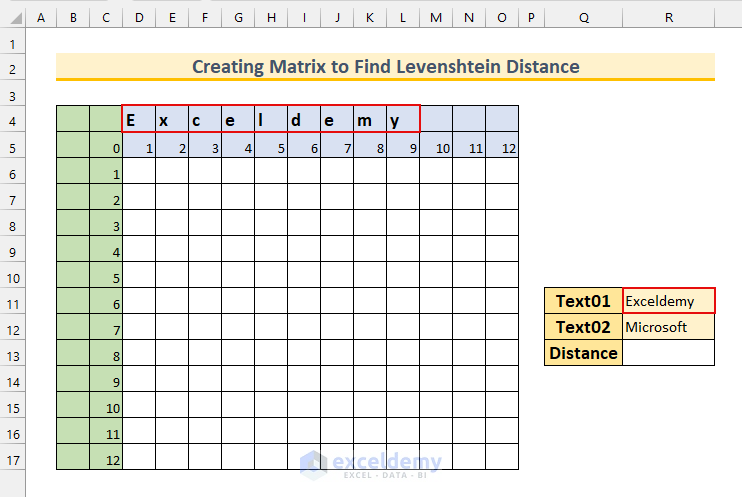
As we want that a similar result for the string “Microsoft” on column “B”:

Select the cell range B6:B17 and enter this formula:

=MID($R$12,C6,1)

Again, the MID function returns a number of characters from a value. Here, the value of cell C6 is 1. Therefore, we are telling the function to return the first character from the “Microsoft” string. Hence, we will get “M” as the output.

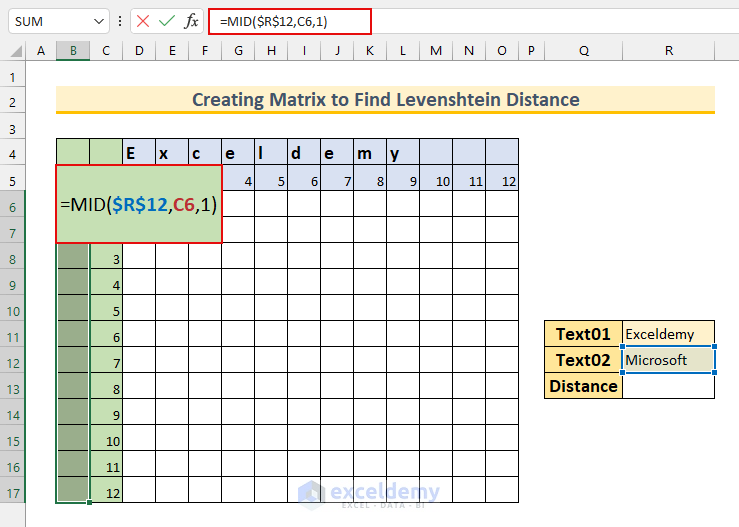
Next, press CTRL+ENTER, which will AutoFill our formula to the selected cells.

Let’s enter another formula.

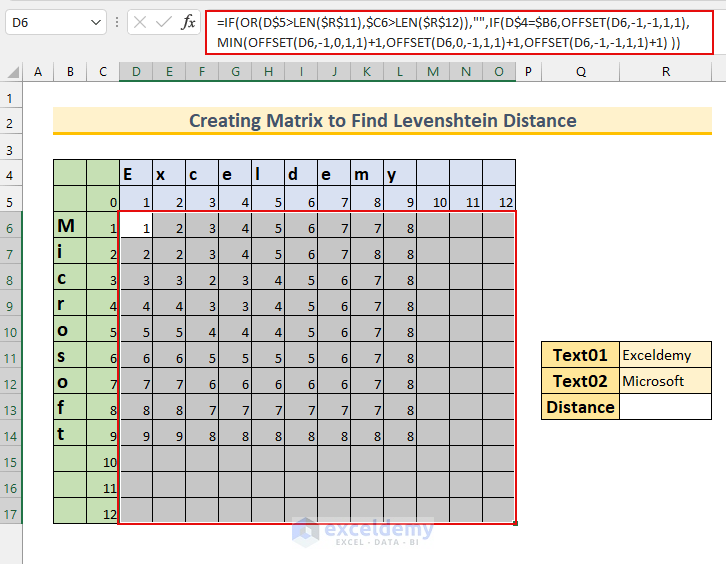
Select the cell range D6:O17 and enter this formula:

=IF(OR(D$5>LEN($R$11),$C6>LEN($R$12)),"",IF(D$4=$B6,OFFSET(D6,-1,-1,1,1), MIN(OFFSET(D6,-1,0,1,1)+1,OFFSET(D6,0,-1,1,1)+1,OFFSET(D6,-1,-1,1,1)+1) ))

Formula Breakdown

We are using nested IF functions here. The first part checks if our value lengths are more than the Matrix size or not. If it is, then we will output a blank cell. Else, another IF function will kick in.
OR(D$5>LEN($R$11),$C6>LEN($R$12))
- Output: FALSE.
- We check whether both strings are more than the row and column number respectively. The value of D5 and C6 both are 1, and the length of the strings is more than 1 too. Therefore it will provide False output, meaning the next part of the formula will run.
Then we check if the single character of the two strings matches by position.
IF(D$4=$B6,OFFSET(D6,-1,-1,1,1), MIN(OFFSET(D6,-1,0,1,1)+1,OFFSET(D6,0,-1,1,1)+1,OFFSET(D6,-1,-1,1,1)+1) )
- Output: 1.
- Here we check whether the strings match or not. As our first character does not match, the MIN portion will execute. From that part, we get MIN(2,2,1). The smallest value is 1. Therefore the output is 1.

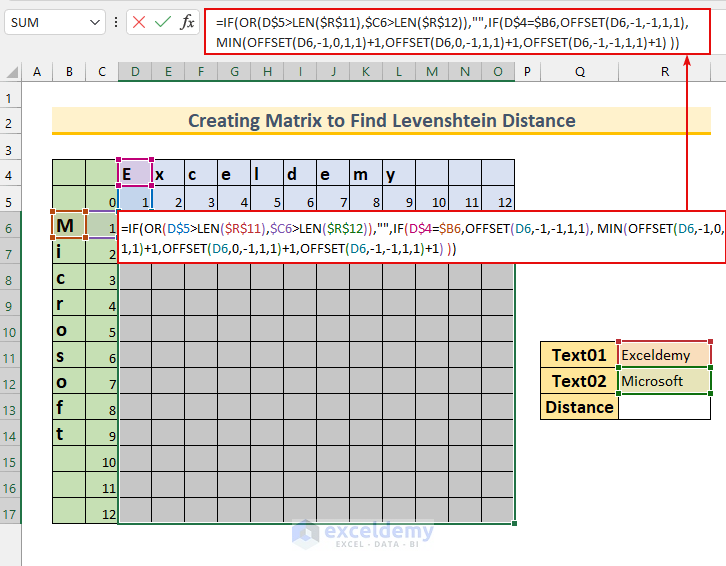
Press CTRL+ENTER, which will AutoFill our formula to the selected cells.

Let’s enter another formula.

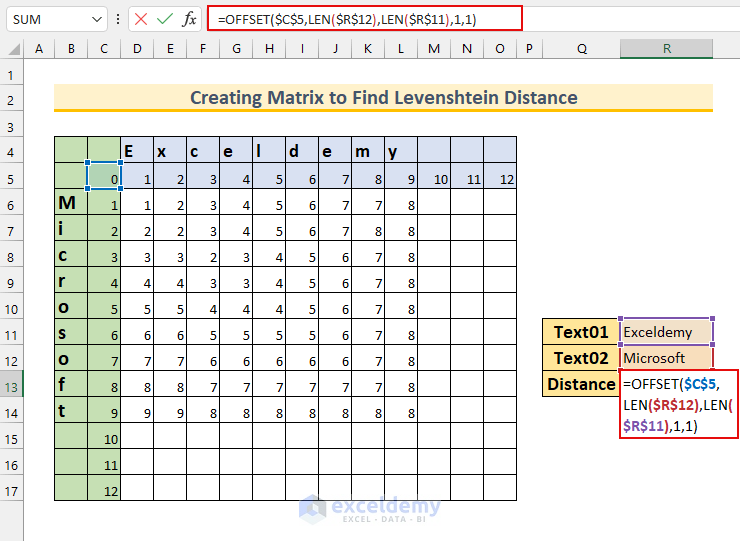
Enter this formula in cell R13:

=OFFSET($C$5,LEN($R$12),LEN($R$11),1,1)

Formula Breakdown

The LEN function returns the string lengths.
Our formula reduces to -> OFFSET($C$5,9,9,1,1)
- Output: 8.
- Our reference point is cell C5. From that cell, it will move 9 cells down and then 9 cells to the right. The two ones at the end refer to the height and width of the reference. This refers to cell L14, which has the value 8, the output returned.

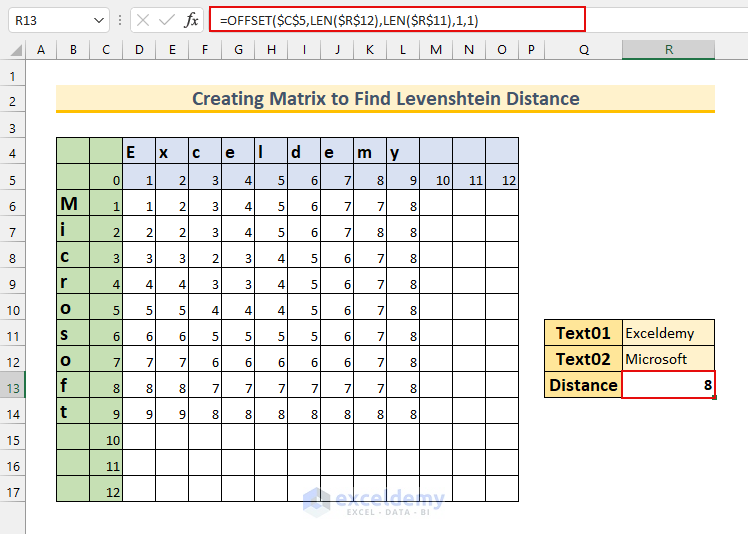
Press ENTER.

This will calculate the Levenshtein distance as 8, meaning we need to perform 8 changes to make both strings the same.

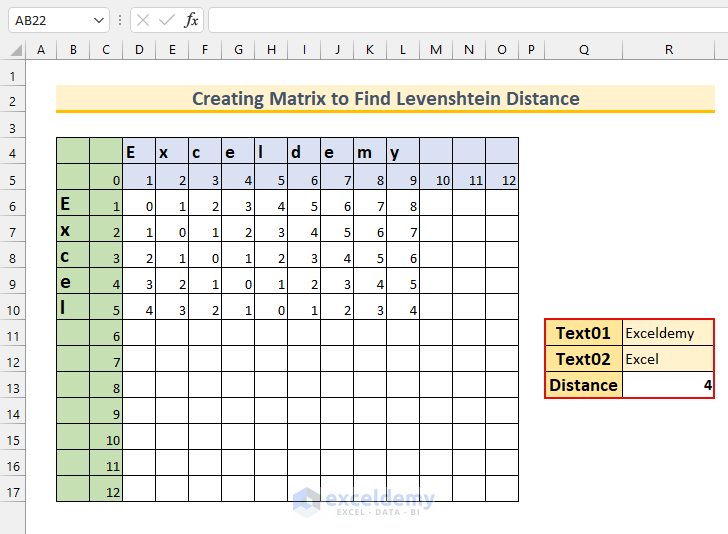
Additionally, we can change the strings to verify that our Matrix works perfectly to calculate the distance.

Method 3 – Using LAMBDA Function

The LAMBDA function allows us to create a custom function without using VBA. However, this function is only available on Microsoft 365.

Steps:

From the Formulas tab, select Name Manager.

A window will appear.

Select New.

Another window will appear.

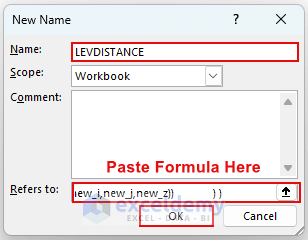
Enter “LEVDISTANCE” in the Name field.
Enter this formula in the “Refers to” field:

=LAMBDA(x,y,[p],[q],[z],
        LET(
            i,IF(ISOMITTED(p),1,p),
            j,IF(ISOMITTED(q),1,q),
            x_i,MID(x,i,1),
            y_j,MID(y,j,1),
            init_array,MAKEARRAY(
                    LEN(x)+1,
                    LEN(y)+1,
                    LAMBDA(r,c,IFS(r=1,c-1,c=1,r-1,TRUE,0))
                    ),
            qq,N(NOT(x_i=y_j)),
            this_z,IF(ISOMITTED(z),init_array,z),
            option_x,INDEX(this_z,i+1-1,j+1)+1,
            option_y,INDEX(this_z,i+1,j+1-1)+1,
            option_c,INDEX(this_z,i+1-1,j+1-1)+qq,
            new_val,MIN(option_x,option_y,option_c),
            overlay,MAKEARRAY(
                    LEN(x)+1,
                    LEN(y)+1,
                    LAMBDA(r,c,IF(AND(r=i+1,c=j+1),new_val,0))
                    ),
            new_z,this_z+overlay,
            new_i,IF(i=LEN(x),IF(j=LEN(y),i+1,1),i+1),
            new_j,IF(i<>LEN(x),j,IF(j=LEN(y),j+1,j+1)),
            is_end,AND(new_i>LEN(x),new_j>LEN(y)),
            IF(is_end,new_val,LEVDISTANCE(x,y,new_i,new_j,new_z))
            )
)

Here, we are creating a LAMBDA function called “LEVDISTANCE”. It has 5 arguments, and of those only 2 are mandatory. We are mainly implementing the Wagner-Fischer algorithm to find out the Levenshtein distance here.

Press OK.

Now, our LAMBDA function is ready. We can start typing inside our dataset to calculate the Levenshtein distance.

Enter the following formula in cell E5:

=LEVDISTANCE(C5,D5)

This function finds the Levenshtein distance between two strings.

Press ENTER.

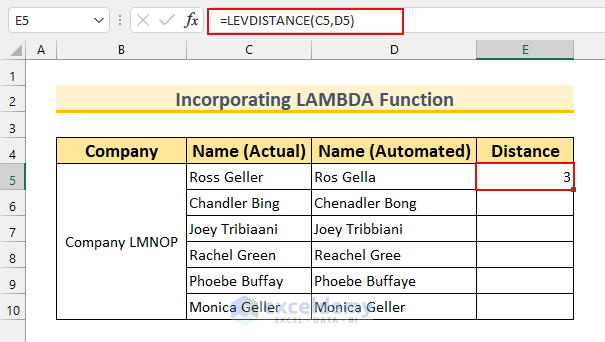
After we AutoFill the formula, our output looks like this:

Method 4 – Using VBA

Steps:

As shown in method 1, bring up the VBA Module.
Enter this code inside the Module:

Sub L_Distance()
Dim p As String, q As String
    Application.ScreenUpdating = False
    With Sheets("VBA")
        For t = 5 To 10
            If Trim(.Cells(t, "C").Value) = Trim(.Cells(t, "D").Value) Then
                .Cells(t, "E").Value = 1
                GoTo Done
            End If
            p = Trim(.Cells(t, "C").Value)
            q = Trim(.Cells(t, "D").Value)
            Len1 = Len(p)
            Len2 = Len(q)
            Same = 0
            For z = 1 To Len2
                If InStr(1, p, Mid(q, z, 1), 1) Then
                    Same = Same + 1
                    p = Replace(p, Mid(q, z, 1), "*", 1, 1)
                End If
            Next z
            .Cells(t, "E").Value = Same / Len1
Done:
            p = LCase(.Cells(t, "C"))
            q = LCase(.Cells(t, "D"))
            maxlen = IIf(Len(p) > Len(q), Len(p), Len(q))
            .Cells(t, "F").Value = (maxlen - VBA_Lev_Distance(p, q)) / maxlen
        Next t
    End With
    Application.ScreenUpdating = True
End Sub

Public Function VBA_Lev_Distance(p As String, q As String)
Dim L_D() As Long, x As Long, y As Long, z As Long, v As Long, w As Long
    x = Len(p)
    y = Len(q)
    ReDim L_D(0 To x, 0 To y)
    For z = 1 To x
        L_D(z, 0) = z
    Next z
    For v = 1 To y
        L_D(0, v) = v
    Next v
    For v = 1 To y
        For z = 1 To x
            w = IIf(Mid(p, z, 1) = Mid(q, v, 1), 0, 1)
            L_D(z, v) = WorksheetFunction.Min(L_D(z - 1, v) + 1, _
            L_D(z, v - 1) + 1, L_D(z - 1, v - 1) + w)
        Next z
    Next v
    VBA_Lev_Distance = L_D(x, y)
End Function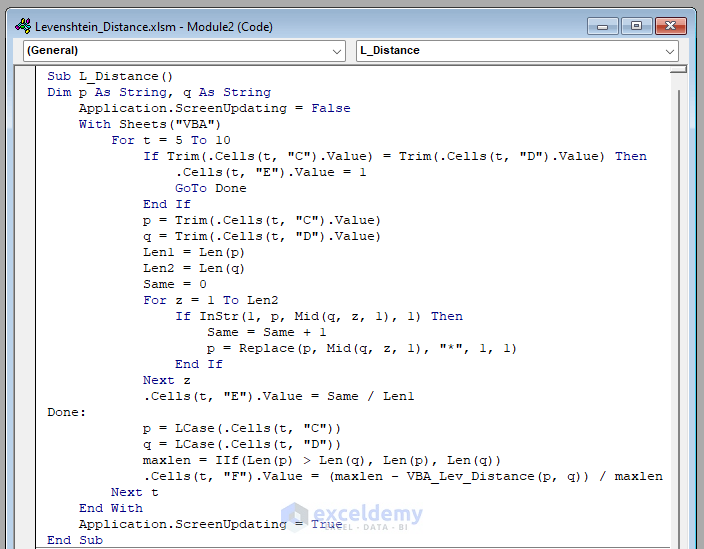

This is the second part of the code:

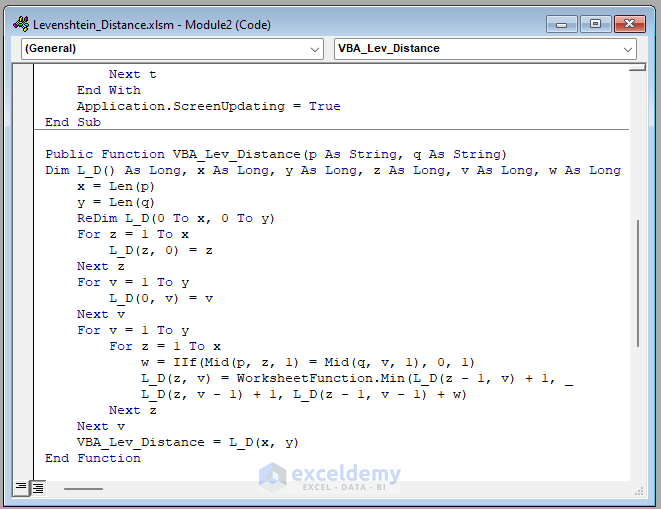
VBA Code Breakdown

We call our Sub Procedure L_Distance.
We define the variable types.
We set our Sheet as “VBA”.
We use the For Next Loop to go through all alphabets in our strings.
We call a function named VBA_Lev_Distance.
We declare the variable types and use another For Next Loop to find the Levenshtein distance.

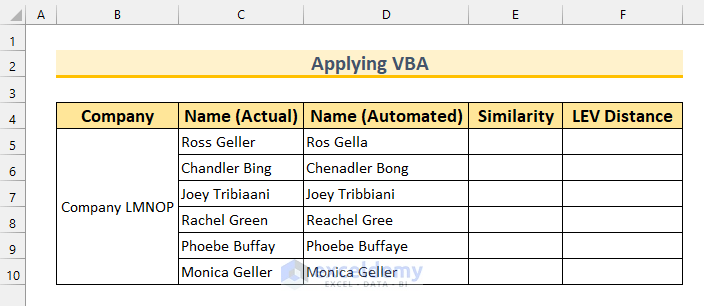
This is what our original dataset looks like:

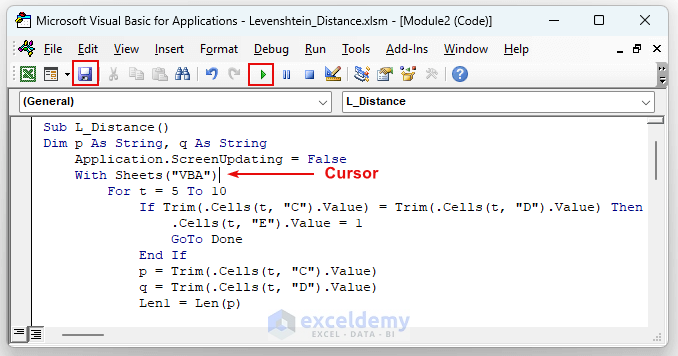
Now, we will execute our code.

Save this Module.
Click inside our code.
Press the Run button.

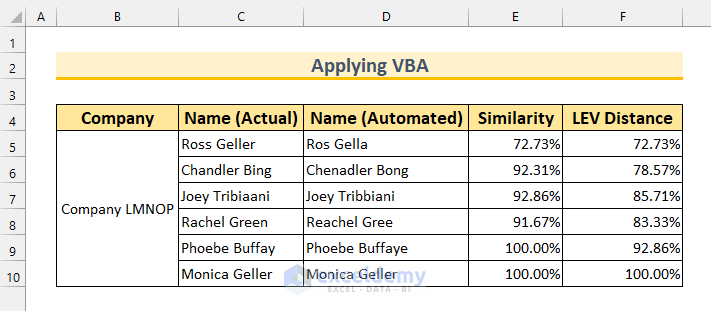
After executing the code, Excel will tell us the normal similarity between the two strings in column E, and the Levenshtein distance similarity in column F.