How to Calculate the Mahalanobis Distance in Excel – Step by Step

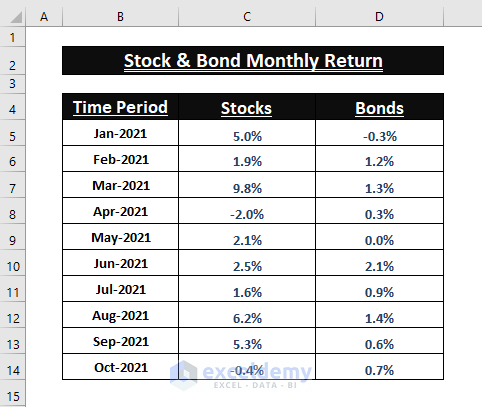
The dataset showcases the monthly return percentages of Stocks and Bonds.

What Is the Mahalanobis Distance?

The Mahalanobis Distance (D_M) refers to the distance between a point and a distribution. It doesn’t mean the typical distance between two specific points. It’s the multivariate equivalent of the Euclidean distance. The Mahalanobis Distance (D_M) is often used in Statistics applications. The formula to calculate the Mahalanobis Distance (D_M) is:

In the formula:

X = the vector observation

µ = the vector Mean of the observations

S^-1 = inverse Covariance matrix

Steps to Calculate Mahalanobis Distance in Excel

There are several components of the Mahalanobis Distance (D_M) formula that need to be computed before calculating the Mahalanobis Distance (D_M):

(i) Calculating Mean (µ)

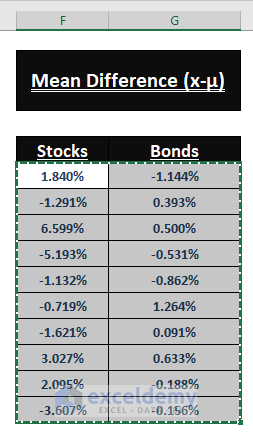
(ii) Calculating Mean Difference (x-µ)

(iii) Finding Covariance Matrix (S)

(iv) Transposing the Mean Difference ((x-µ)^T)

(v) Finding Inverse Covariance Matrix (1/S)

(vi) Multiplying Mean Difference (x-µ) and Inverse Covariance Matrix (1/S)

(vii) Multiplying all Mahalanobis Distance Components ((1/S)*(x-µ)*((x-µ)^T)))

(viii) Mahalanobis Distance (D_M) calculation

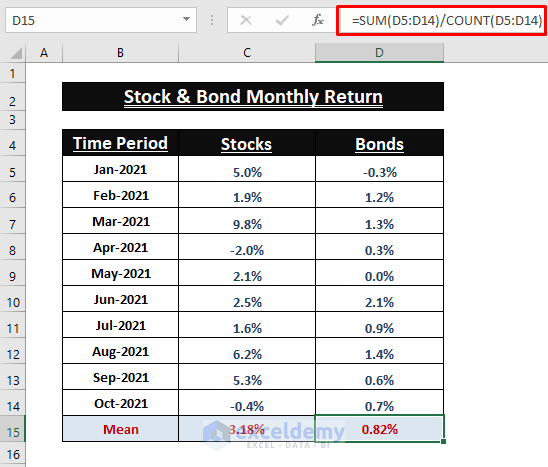
 Calculating Mean (µ) from Values

• Find the Mean. Use the following formula in C15.

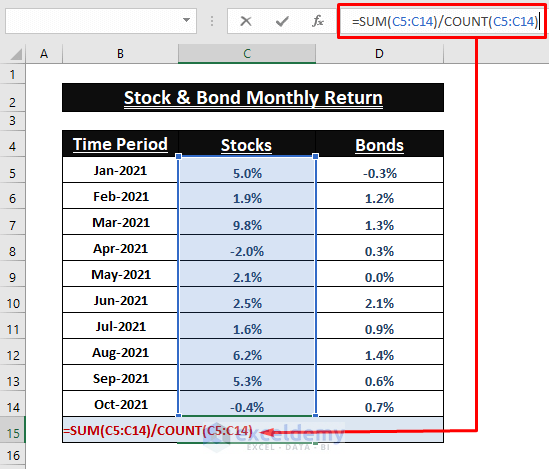
• Use the previous formula to find the Mean for Bonds (Column D).

You can also use the AVERAGE function to find the Mean.

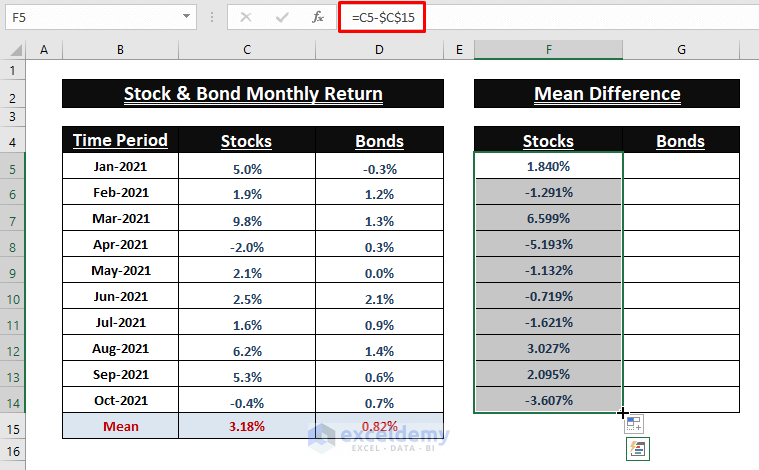
Calculating Mean Difference (x-µ) of Values

• Find the Mean Difference (x-µ) of individual entries. Enter the following formula in F5:

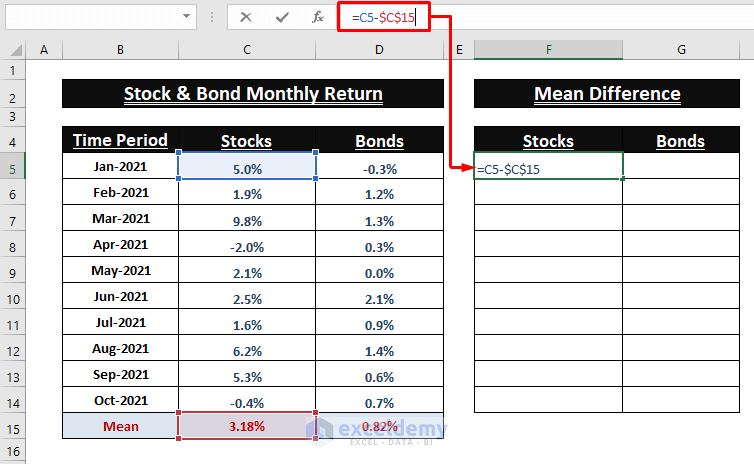
• Use the Fill Handle to apply the formula to the other cells.

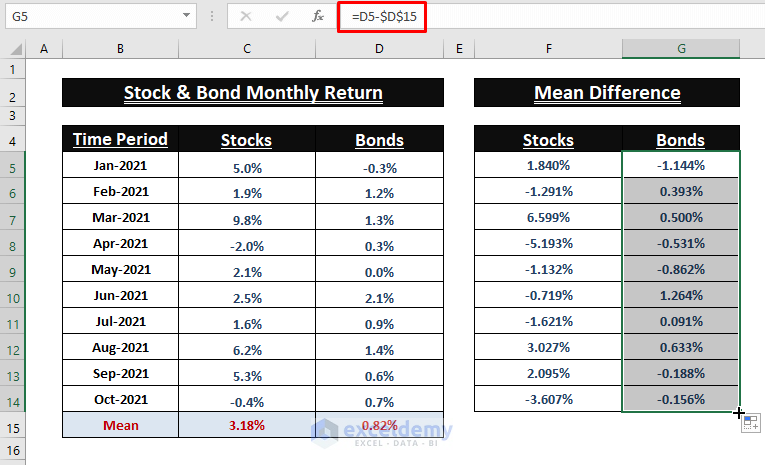
• Repeat the previous steps, using the same formula to find the Mean difference for Bonds (Column G).

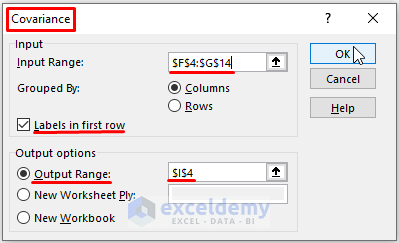
Finding the Covariance Matrix (S) by Using Data Analysis

• Go to the Data tab > in Analysis click Data Analysis.

• In the Data Analysis window, choose Covariance.
• Click OK.

• In the Covariance dialog box, enter F4:G14 (Mean Difference Range) as Input Range, and I4 as Output Range.
• Check Labels in first row.
• Click OK.

The Covariance Matrix(S) is displayed.

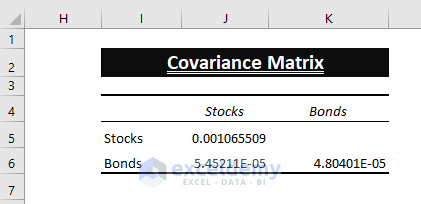
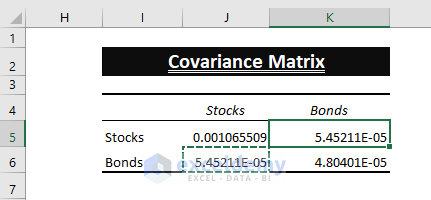
• Excel in-built doesn’t insert all the entries. Therefore, Copy (CTRL+C) and Paste (CTRL+V)  J6 value in K5.

• Use the MINVERSE function to get the Inverse Covariance Matrix.
• Press CTRL+SHIFT+ENTER to enter the formula below. (Make sure the Covariance Matrix is a Square Matrix)

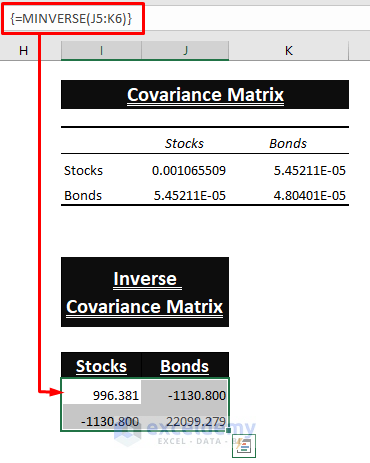
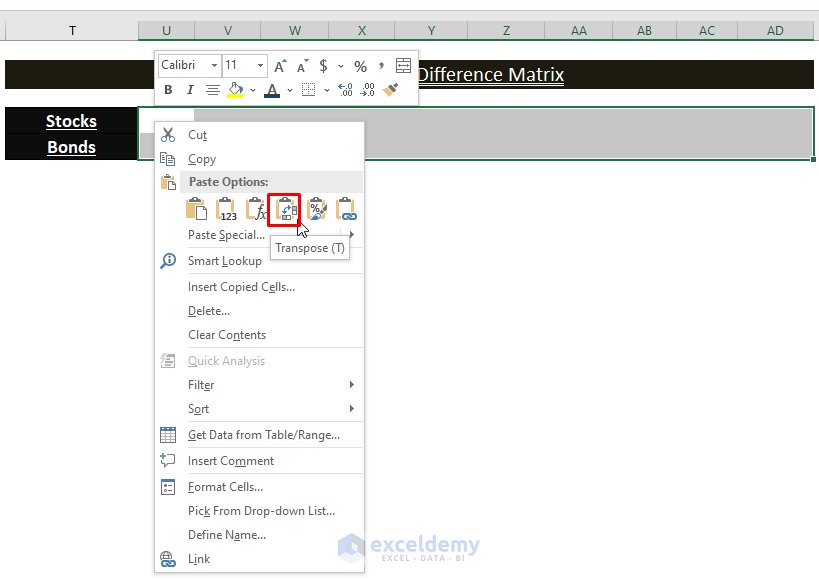
Transposing the Mean Difference Matrix ((x-µ)^T)

• Use the Transpose function or Copy (CTRL+C) the Mean Difference (F5:G14).

• Select any range and right-click it.
• Click Transpose to insert the transposed Mean Difference Matrix (x-µ)^T.

This is the output.

Multiplication of the Inverse Covariance Matrix (1/S) and Mean Difference (x-µ)

• Enter the following formula in I5.

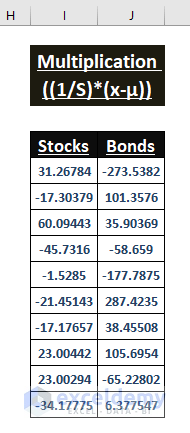
The MMULT function array multiplies the given two arrays.

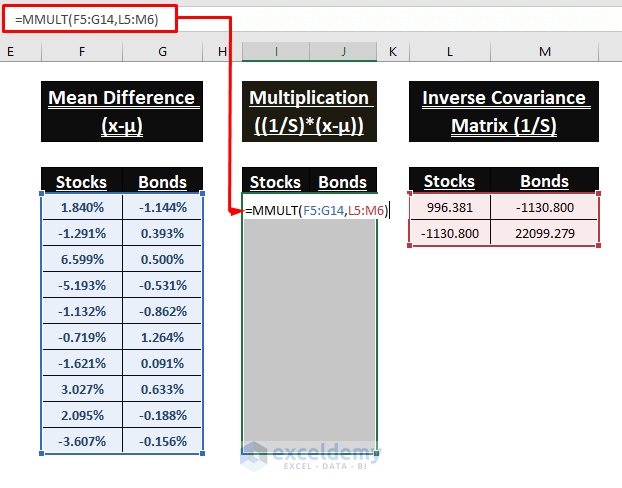
• This is an array formula. Use CTRL+SHIFT+ENTER to enter it.

Multiplication of All Mahalanobis Distance Components ((1/S)*(x-µ)*((x-µ)^T))

•  Use the following formula in N8.

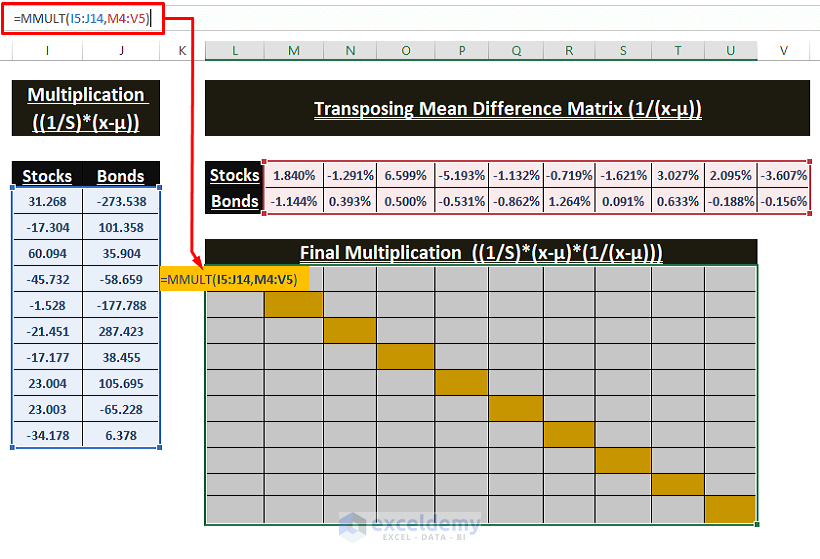
• Press CTRL+SHIFT+ENTER to apply the array formula.

This is the output.

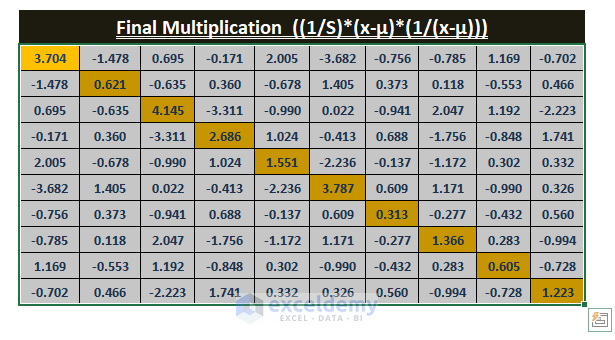
Calculation of the Mahalanobis Distance

• Enter the formula in W3 to find the distance.

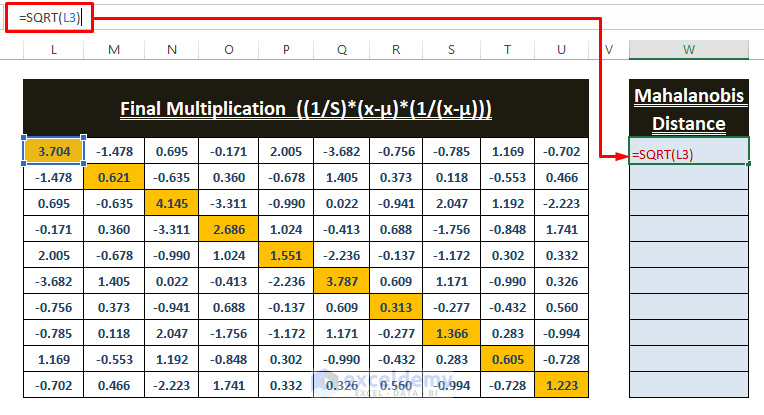
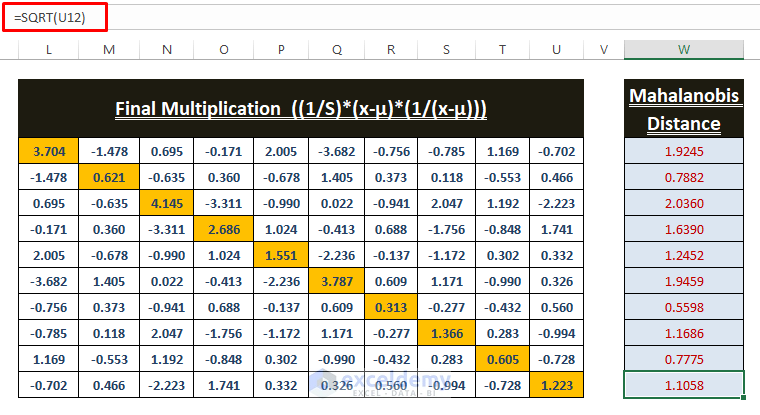
• Use the diagonal values to find the Mahalanobis Distances. Mahalanobis Distance results in #NUM! error if the final multiplication value displays a minus.

Download Excel Workbook

<< Go Back to Distance | Formula List | Learn Excel