Excel Confidence Interval for Difference in Means (2 Examples)

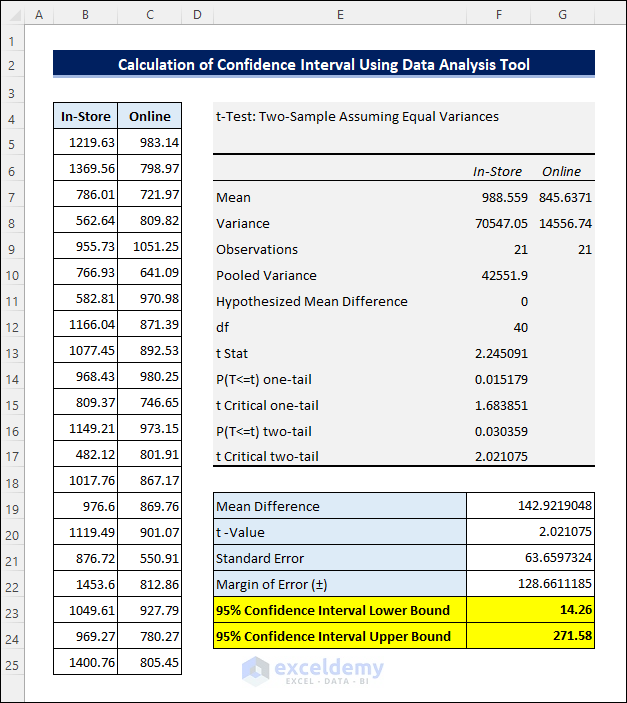
This article illustrates how to calculate the Confidence Interval for a difference in Means in Excel, both by using Excel’s statistical functions and by means of the Data Analysis tool. The following picture shows a sample result obtained from such operations.

What Is a Confidence Interval?

Confidence Interval (CI) is a statistical term referring to a range of values that include a population with an assumed confidence level. It is often used to analyze the statistical significance of a certain estimation, and depends on the sample size, sample variance, and confidence level. Statisticians normally use a 95% confidence level to calculate the confidence interval. This measure is often misunderstood or misinterpreted as saying that 95% of the sample values lie within the confidence interval, although this may not be the case.

Calculating the Confidence Interval in Excel for a Difference in Means: 2 Methods

Suppose we have a bookstore with an online extension and are wondering if the average daily sales through the website of the store are different from the in-store sales. For this purpose, have collected the sales data for 3 weeks both from the in-store and online sales.

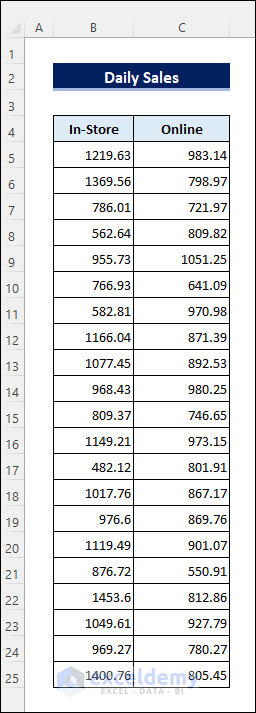
Let’s calculate the confidence interval based on this dataset to draw a conclusion.

Method 1 – Using Formulas to Calculate the Confidence Interval for a Difference in Means

Steps:

First we’ll calculate the Mean of In-Store sales. Then we’ll calculate the Mean of Online sales in a similar way. Finally, we’ll subtract one Mean from the other to derive the Mean Difference.

• Enter the following formula in cell F4 to calculate the Mean of In-Store sales:

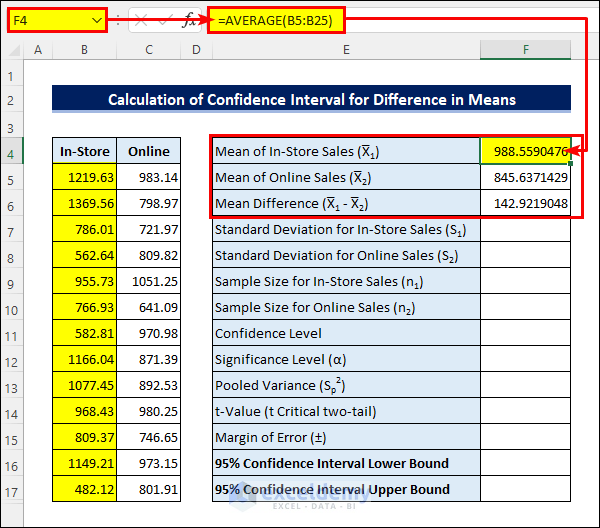
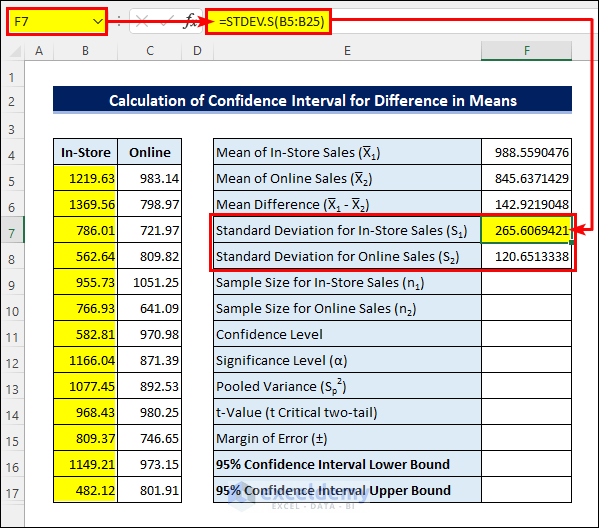
• Enter the following formula in cell F7 to get the Standard Deviation for In-Store sales:

• Calculate the Standard Deviation for Online sales in the same way.

• Enter the Sample Sizes and Significance Level.

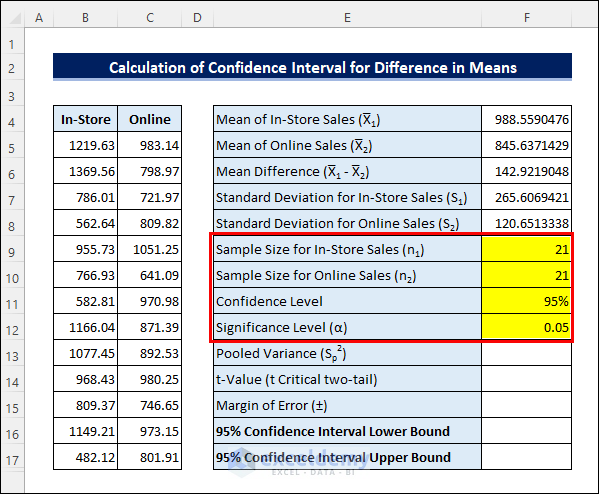
• Apply the following formula in cell F13 to calculate the Pooled Variance:

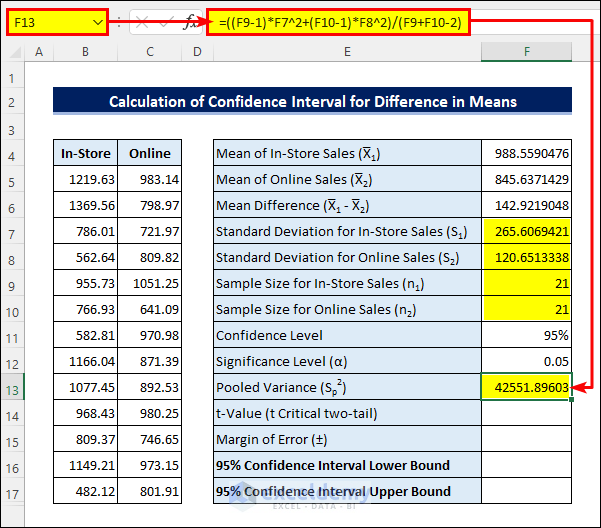
• Enter the following formula in cell F14 to calculate the t-Value:

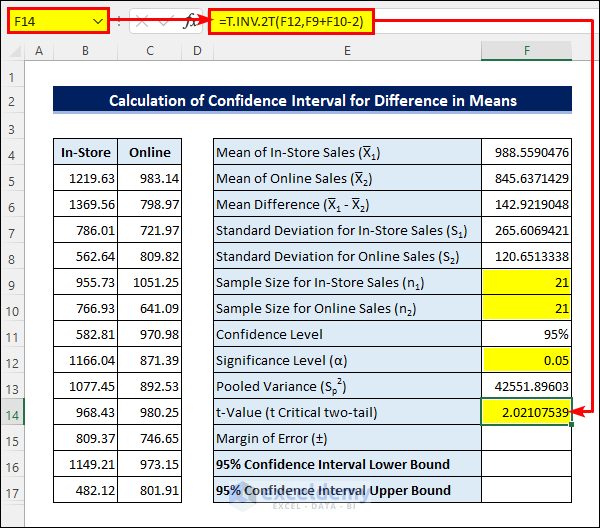
• Apply the following formula in cell F15 to get the Margin of Error:

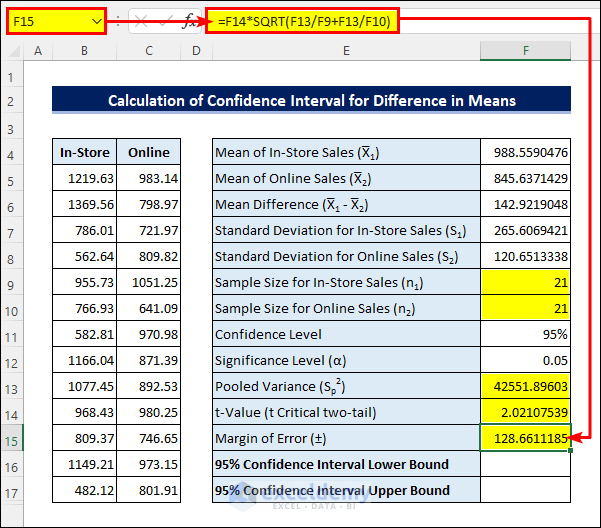
• Finally, subtract the Margin of Error from the Mean Difference to get the Confidence Interval Lower Bound, then add them to get the Upper Bound.

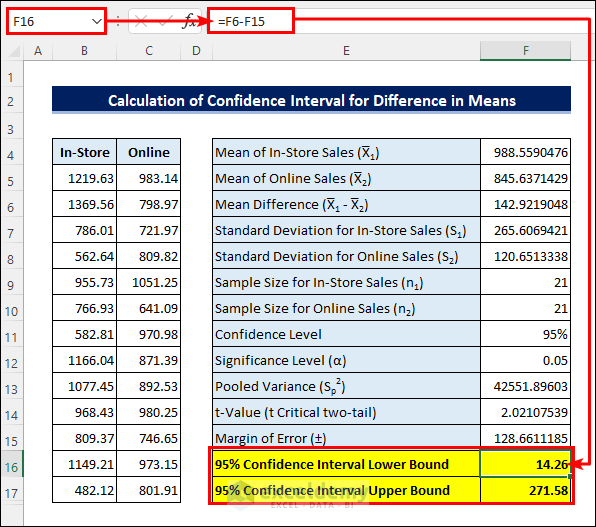
The results suggest that there is a possibility that the Mean for daily In-Store sales will be $14.26 to $271.58 higher than for Online sales.

Method 2 – Using the Data Analysis Tool to Calculate the Confidence Interval for a Difference in Means

Steps:

• If necessary, enable the Analysis Toolpak add-in from File >> Options >> Add-ins >> Go.
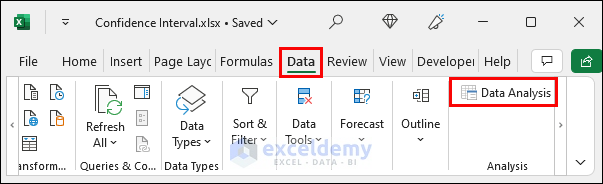
• Select Data >> Data Analysis.

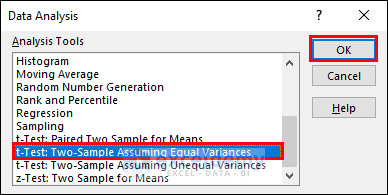
• Choose t-Test: Two-Sample Assuming Equal Variances and click OK.

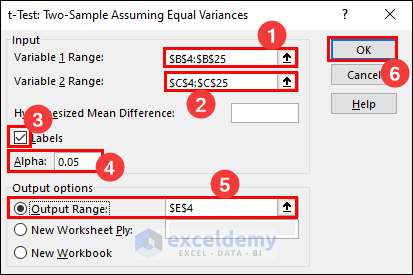
• Select the sample ranges as the Variable 1 Range and Variable 2 Range respectively.
• Check the Labels checkbox and keep the Alpha value as 0.05.
• Enter the output range.
• Click OK.

The following result is returned:

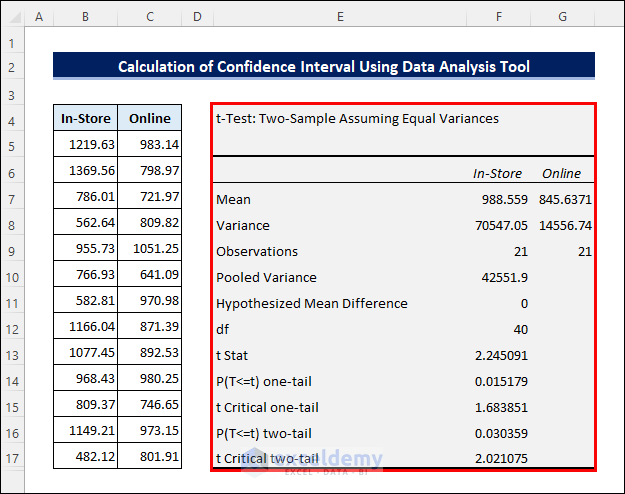
• Calculate the Mean Difference by subtracting the two Means using the t-Value from the analysis.
• Apply the following formula in cell F21 to calculate the Standard Error:

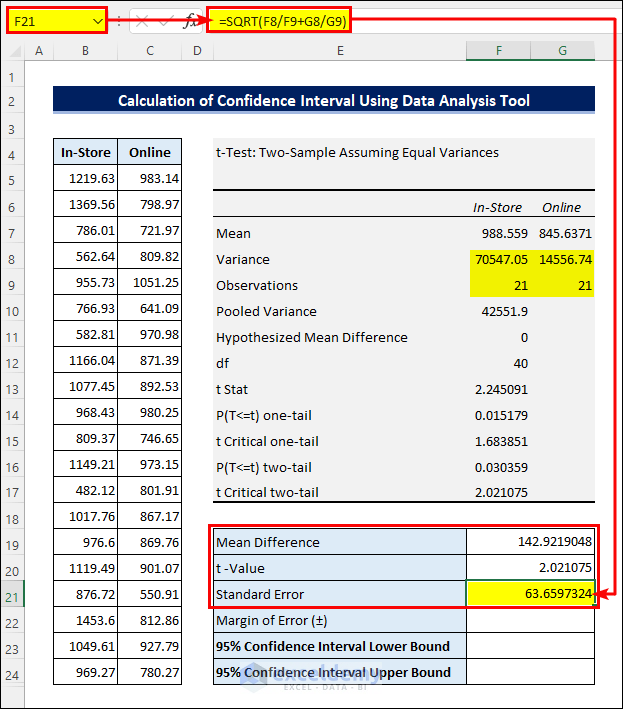
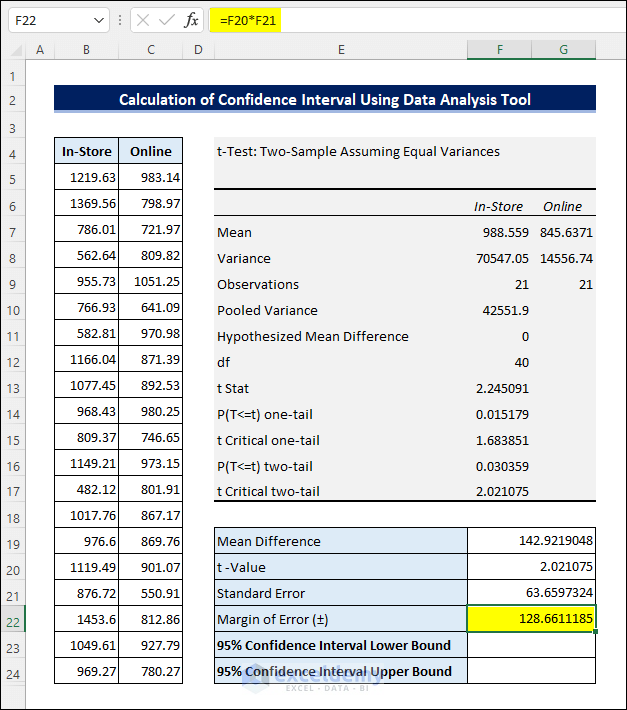
• Multiply the t-Value with the Standard Error to get the Margin of Error.

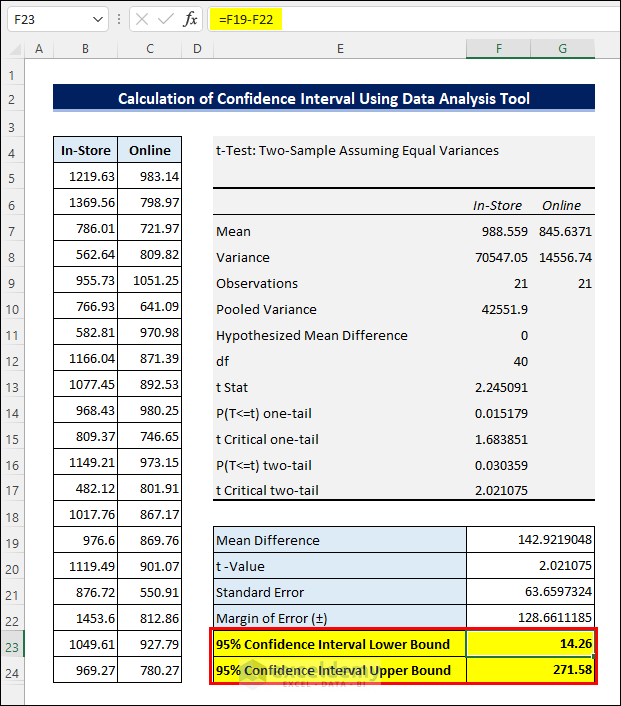
• Finally, calculate the Confidence Interval by adding and subtracting the Margin of Error to and from the Mean Difference as above.

Things to Remember

• Enable the Data Analysis tool from File >> Options >> Add-ins >> Go if it is not enabled already.
• Use a different Confidence Level or assume unequal Sample Variances if required.

Download Practice Workbook

Related Articles

• How to Calculate P-Value from Confidence Interval in Excel
• How to Calculate Population Proportion in Excel
• How to Calculate Confidence Interval Proportion in Excel
• How to Calculate Confidence Interval for Population Mean in Excel

<< Go Back to Confidence Interval Excel | Excel for Statistics | Learn Excel