How to Create a Distribution Chart in Excel: 2 Methods

Method 1 – Creating a Frequency Distribution Chart in Excel

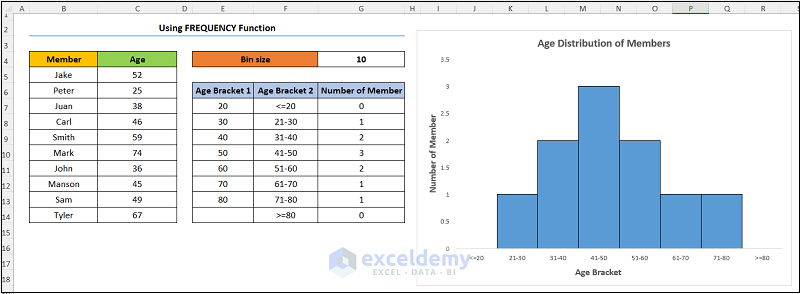
Let’s say we have the information for Oakmont Ridge Golf Club shown in the B4:C14 cells below. Here, the dataset shows the names of the club Members and their Ages.

1.1 Applying FREQUENCY Function to Make Frequency Distribution Chart

Step 1 – Calculate Bins and Frequency

Add a column for the bins, in this case, Age Bracket 1.
Let’s set the starting value (E7) of the bin to 20. In addition, we chose a Bin Size of 10.
Enter the expression given below into E8:

=E7+$G$4

Here, the E7 and the G4 cells represent the Age Bracket 1 and Bin Size respectively.

It is important to note that you must lock the G4 cell reference with the F4 key on your keyboard.

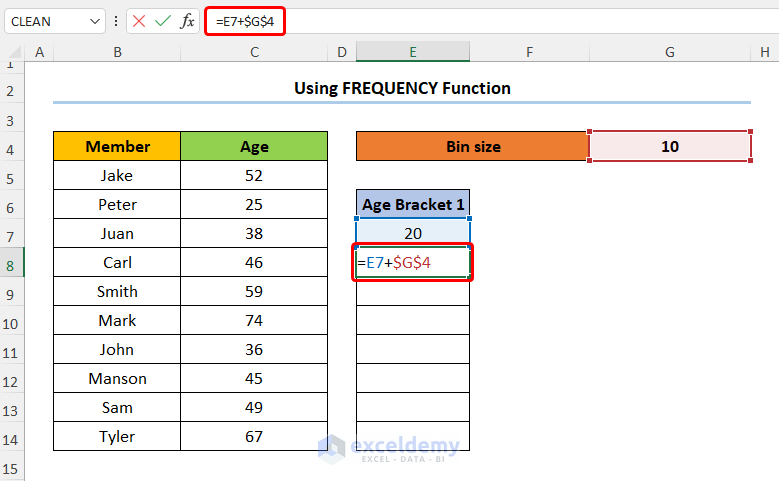
Drag the fill handle from E8 to E14.
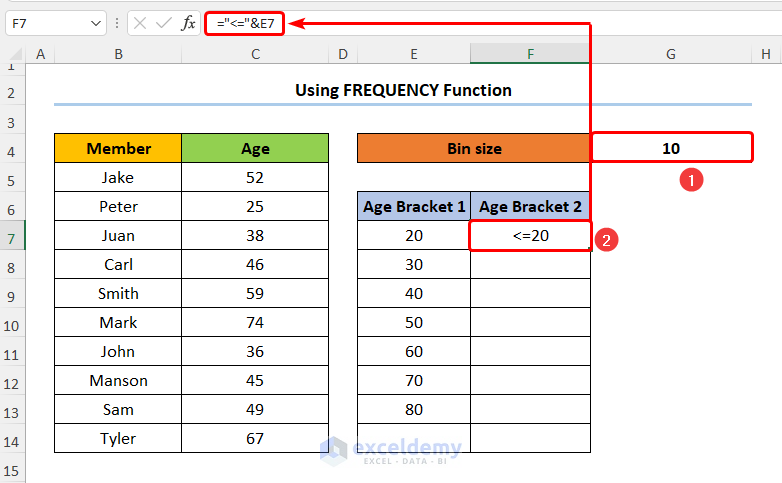
Put the following first calculation the Age Bracket 2 into F7 shown below:

="<="&E7

In the above formula, we combine the less-than-equal sign (“<=” ) with the E7 cell using the Ampersand (&) operator.

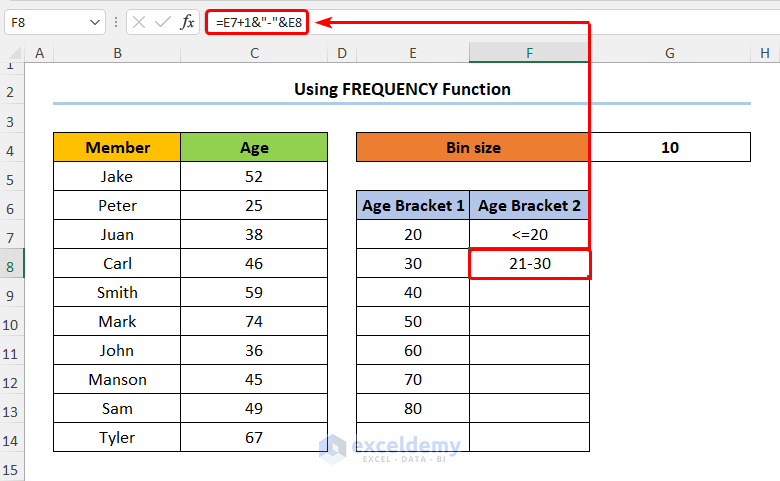
Type in the expression given below into F8:

=E7+1&"-"&E8

In this expression, the E8 cell refers to Age Bracket 1.

Add the frequency column with the header Number of Member and enter this formula:

=FREQUENCY(C5:C14,E7:E13)

In the above formula, the C5:C14 and the E7:E13 cells indicate the Age and the Age Bracket 1 columns respectively.

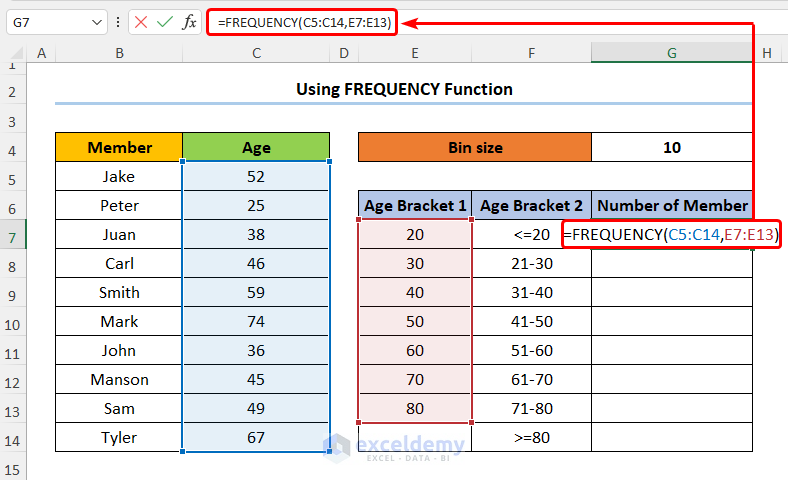
Step 2 – Insert the Chart and Add Formatting

Select the Age Bracket 2 and the Number of Member columns.
Go to Insert then to Insert Column or Bar Chart.
Select Clustered Column.

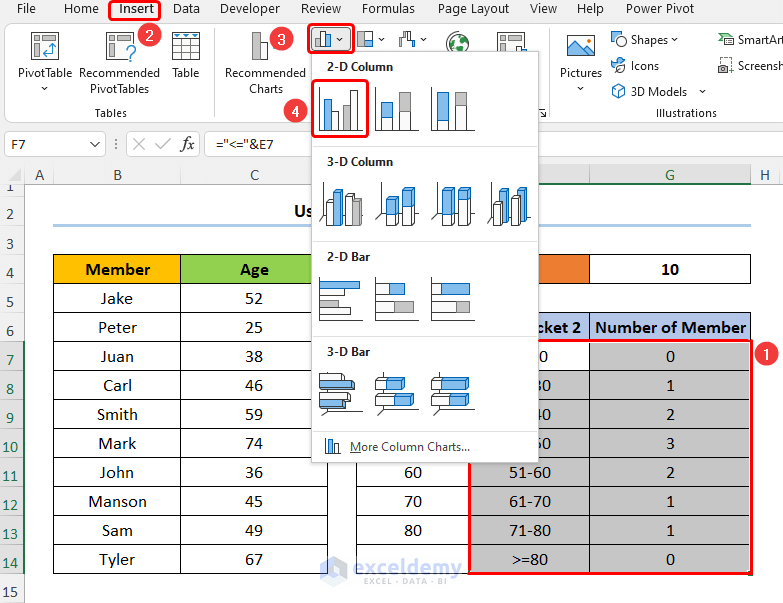
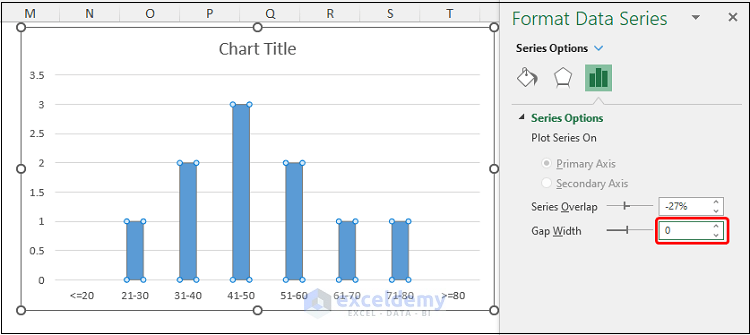
Double-click on any of the bars to open the Format Data Series window.
Set the Gap Width to 0%.

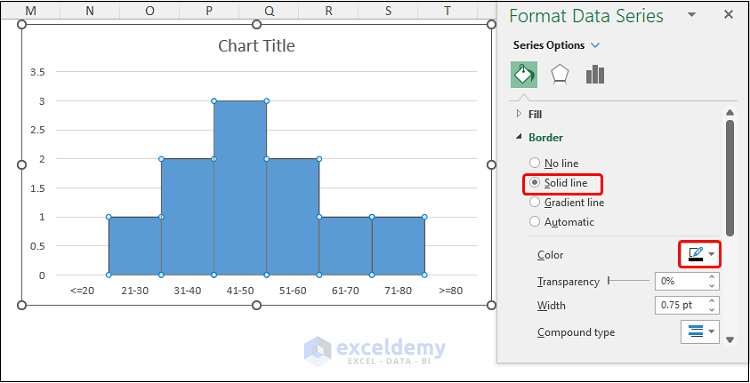
Go to Border > Solid Line and choose a Color. We chose Black.

Insert Axis Titles from the Chart Elements option.

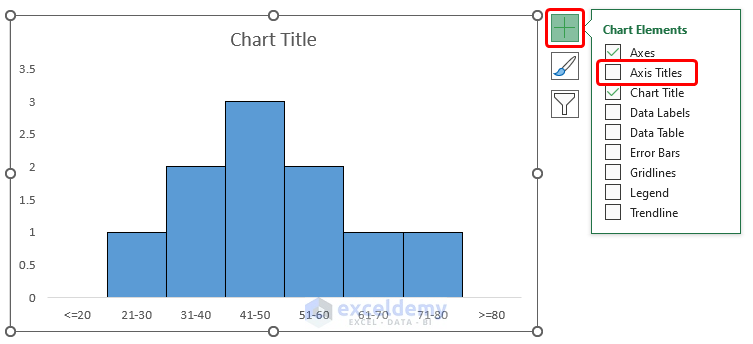
The results should look like the below image.

1.2 Using Data Analysis ToolPak to Create Frequency Distribution Chart

Steps:

Navigate to File and Excel Options.

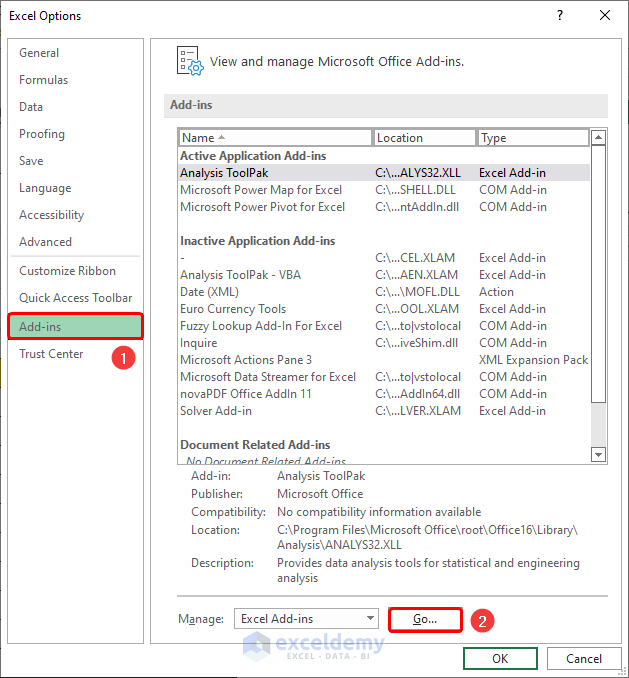
A dialog box opens. Click the Add-ins and then the Go button.

Choose the Analysis ToolPak option and click OK.

Go to Data, then to Data Analysis.

Choose the Histogram option.

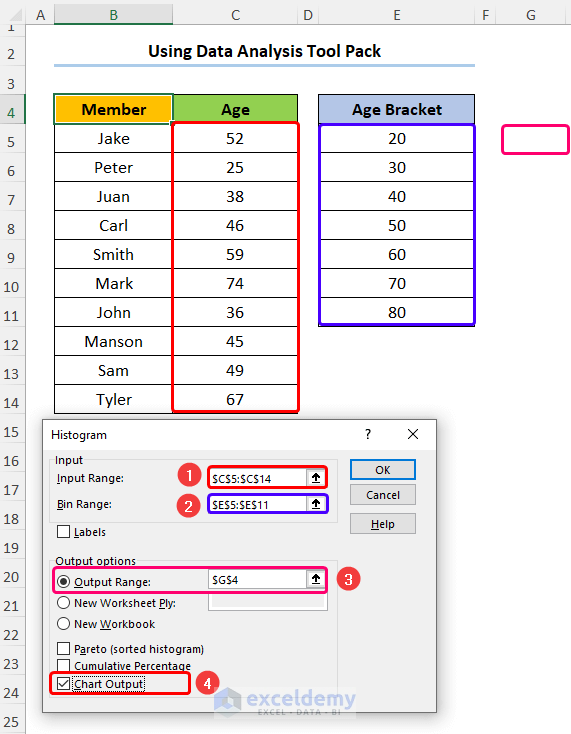
Enter the Input Range, Bin Range, and Output Range as shown below.
Check the Chart Output option.

You should get the following output as shown in the screenshot below.

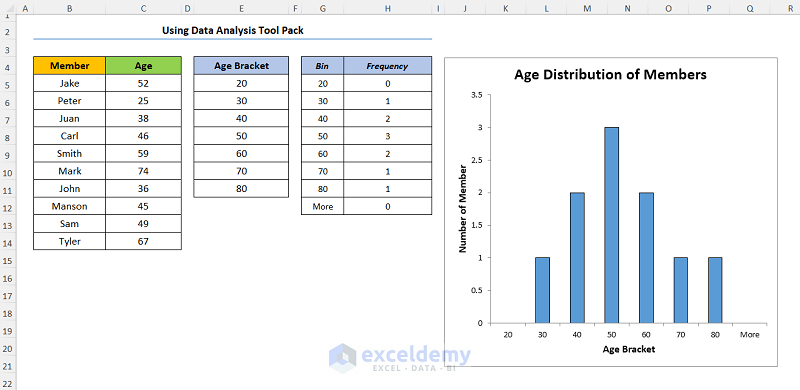
1.3 Inserting Frequency Distribution Chart Pivot Table

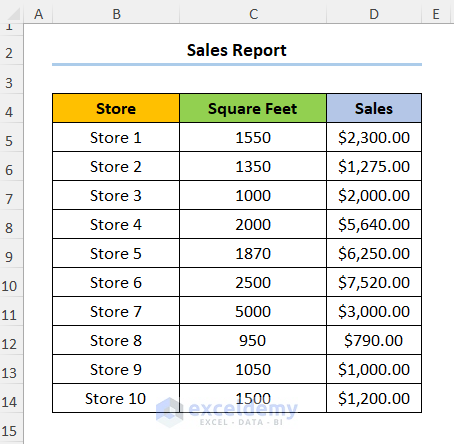
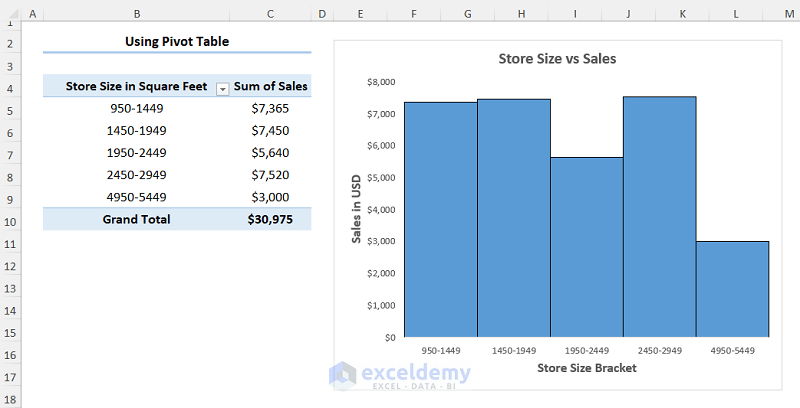
Consider the Sales Report dataset shown below in the B4:D14 cells: the first column indicates the Store number, following that we have the store size in Square Feet, and lastly, we have a column for the Sales amount in USD.

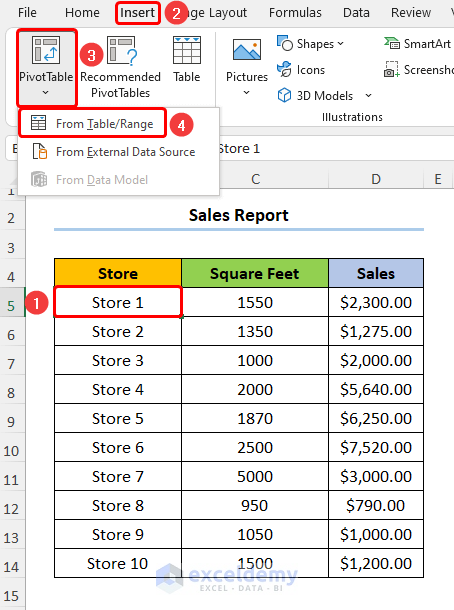
Step 1 – Insert a Pivot Table and Group Data

Select any cell within the dataset and go to Insert, PivotTable, and From Table/Range.

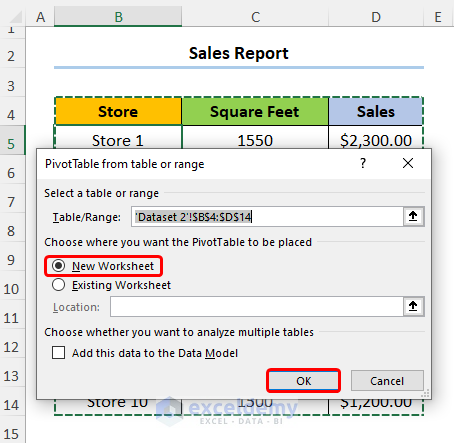
Check the New Worksheet option and press OK.

On the PivotTable Fields pane, drag the Square Feet and Sales fields into the Rows and Values area respectively.

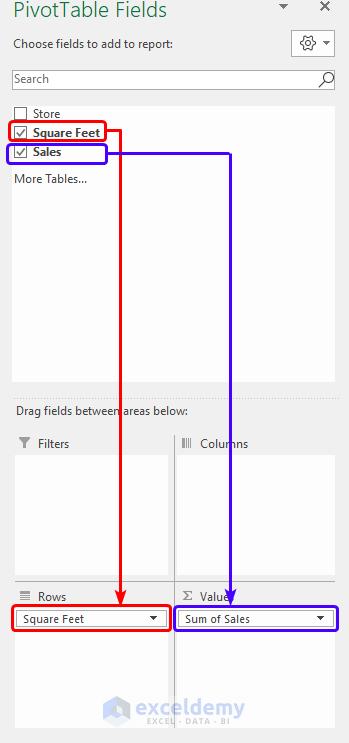
You’ve made a PivotTable.

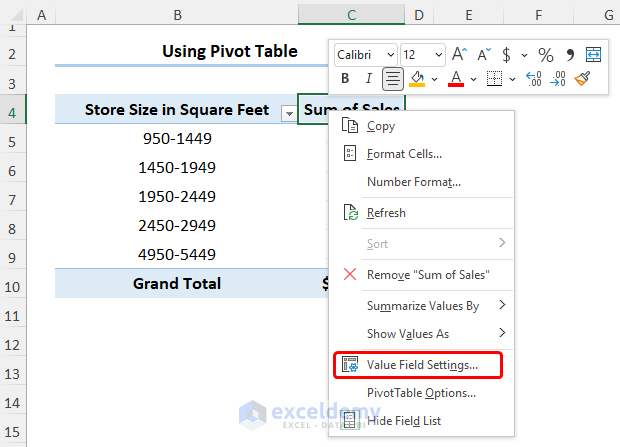
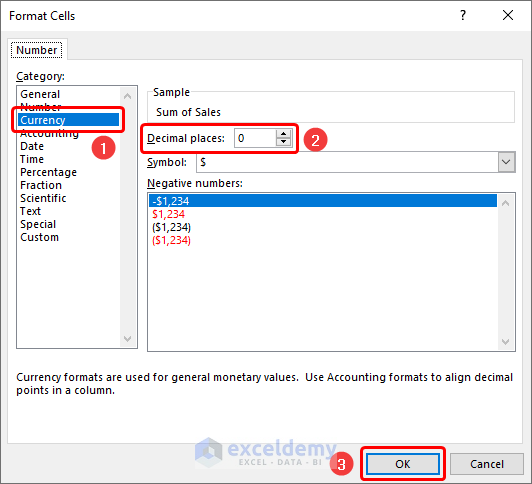
You can format the numeric values by right-clicking and selecting the Field Value Settings.

Click the Number Format button.

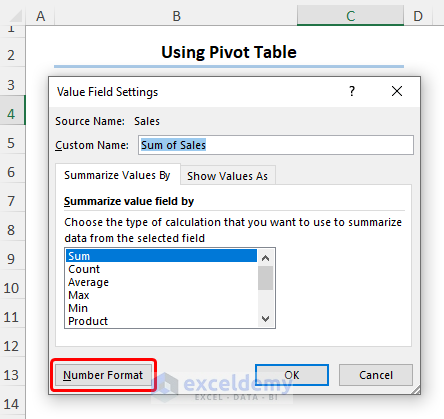
Choose the Currency option. In this case, we chose 0 decimal places for the Sales value.

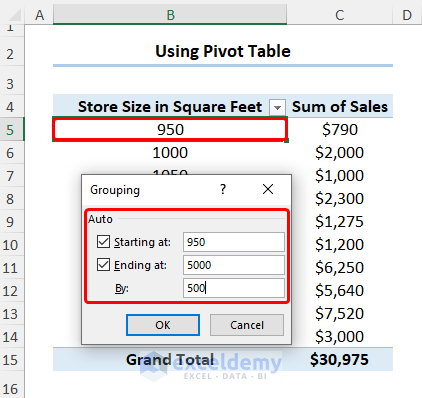
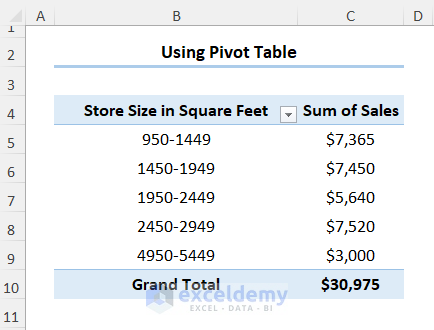
Select any cell in the PivotTable and right-click to go to Group Data.
We now want to group the store size into bins. Enter the start value (Starting at), the end value (Ending at), and the interval (By).

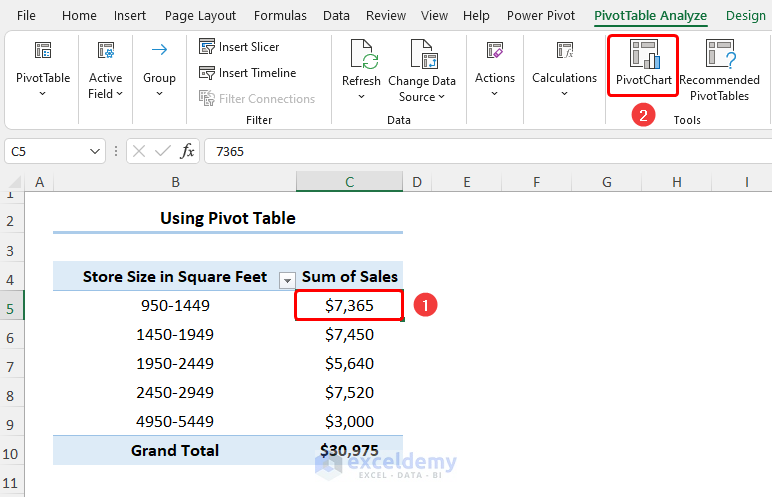
Step 2 – Insert Histogram

Select any cell in the PivotTable and go to PivotChart.

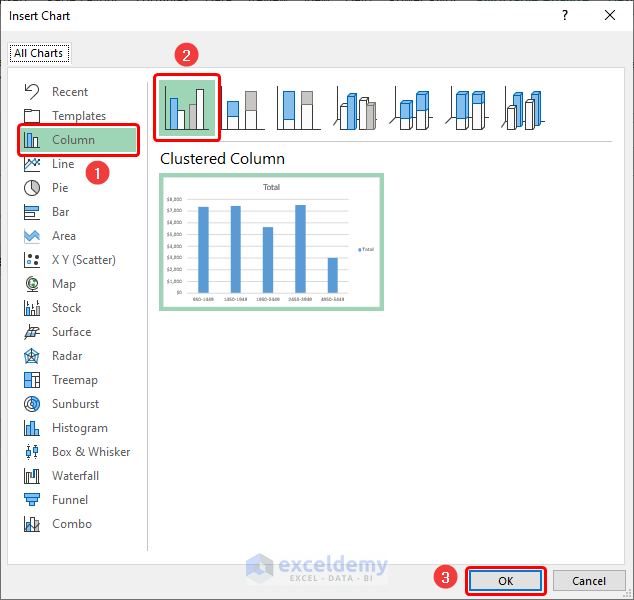
Choose Column then the Clustered Column chart.

Add formatting to the chart using the Chart Elements option.

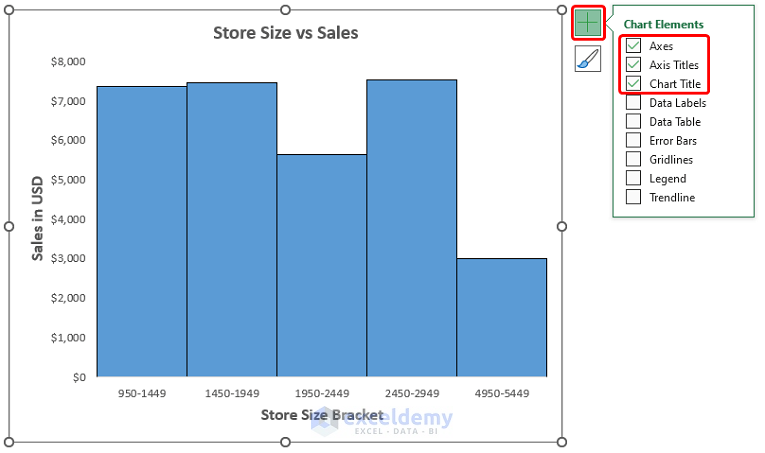
The resulting Histogram should look like the image shown below.

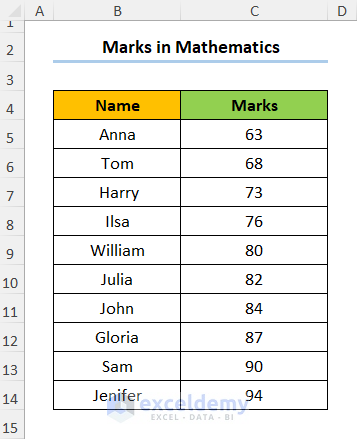
Method 2 – Making a Normal Distribution Chart with NORM.DIST Function in Excel

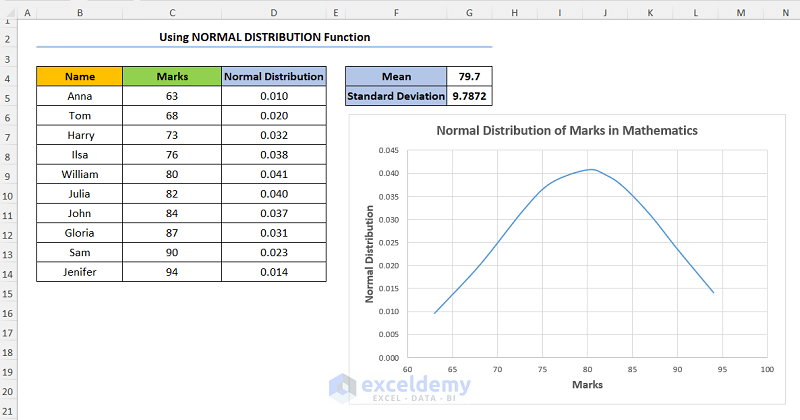
Consider the dataset shown below where the student Names and their corresponding Marks in Mathematics are provided.

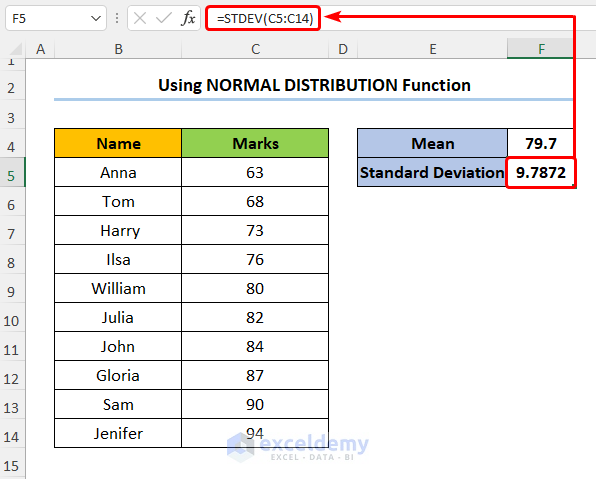
Step 1 – Calculate Mean and Standard Deviation

Create two new rows for the Mean and Standard Deviation.
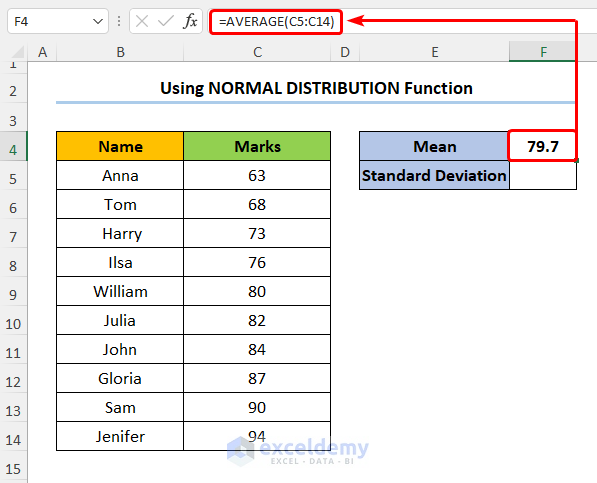
Enter the formula shown below into Mean to compute the mean Marks:

=AVERAGE(C5:C14)

In this formula, the C5:C14 cells point to the Marks. Moreover, we use the AVERAGE function to obtain the mean Marks.

Type in the formula for Standard Deviation of the Marks:

=STDEV(C5:C14)

Here, we’ve used the STDEV function to get the Standard Deviation.

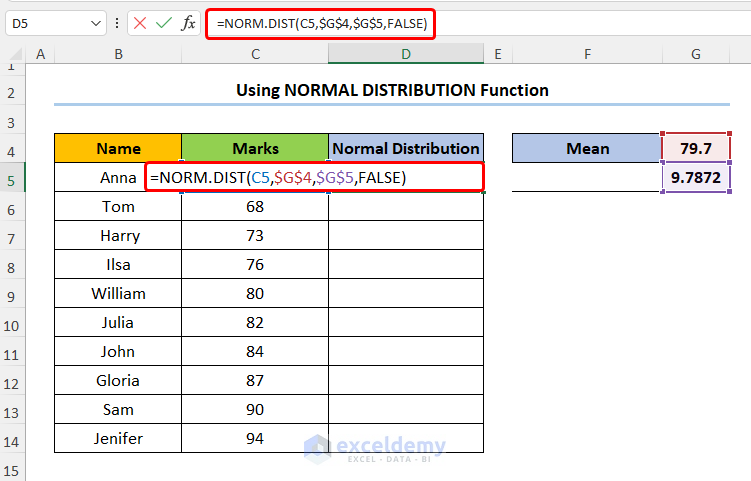
Insert a new column D.
Calculate the values of the Normal Distribution Table using the NORM.DIST function into D5:

=NORM.DIST(C5,$G$4,$G$5,FALSE)

In this expression, the C5 cell (x argument) refers to the Marks column. Next, the G4 and G5 cells (mean and standard_dev arguments) indicate the Mean and Standard Deviation values of the dataset. Lastly, FALSE (cumulative argument) is a logical value determining the form of the function.

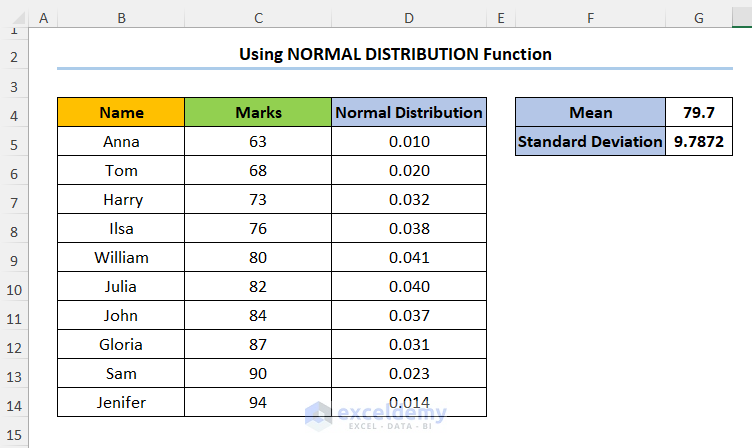
Drag the fill handle from D5 through the column.

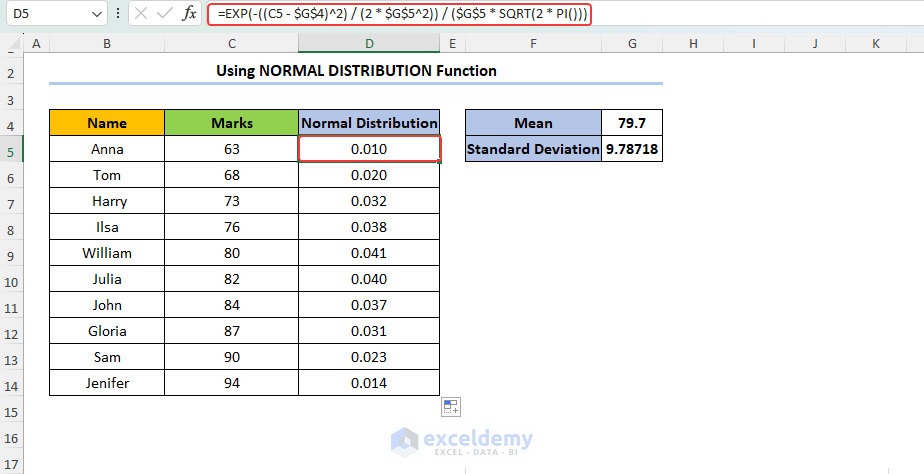
Alternatively, you can determine Normal Distribution using a mathematical formula. To do this, use the following formula in the D5 cell.

=EXP(-((C5 – $G$4)^2) / (2 * $G$5^2)) / ($G$5 * SQRT(2 * PI()))

Here, $G$4 and $G$ represent Mean (μ) and Standard deviation (σ) respectively.

The basis of the above formula is the following mathematical formula:

f(x) = exp(-(x - μ)^2 / (2σ^2))/((σ * √(2π))

Formula Explanation

Now, let’s breakdown our used formula in the D5 cell.

EXP(-((C5 – $G$4)^2) / (2 * $G$5^2)): This formula finds the squared difference between the C5 and G5 cells first. The output is then divided by 2 times squares value of G5 Finally, we use the EXP function to find the exponential value of exp(-(x – μ)^2 / (2σ^2)) according to the mathematical formula.

($G$5 * SQRT(2 * PI())): This formula finds out the value of ((σ * √(2π)). Here $G$5 is σ.

Using the data in the Normal Distribution column create the Normal Distribution Chart like the previous method.

Step 2 – Insert Normal Distribution Chart

Select the Marks and Normal Distribution columns.
Go to Insert, choose Insert Scatter or Bubble Chart, and select Scatter with Smooth Lines.

You should get the outcome as shown in the screenshot below.

Suitable Data Type for Different Distribution Chart

Discrete data: Discrete data refers to information that can only take on specific, separate values, typically represented by whole numbers or distinct categories.
Continuous data: Continuous data refers to information that can take on any value within a specific range or interval. It is measured on a continuous scale and can include fractional or decimal values. Continuous data is not limited to distinct categories or whole numbers.

Distribution Type	Data Type	Example
Normal Distribution	Continuous numerical data that follows a bell-shaped curve.	Heights of individuals, IQ scores
Uniform Distribution	Continuous numerical data that is evenly distributed across a range.	Random number generation, rolling a fair die
Exponential Distribution	Continuous numerical data representing the time between events in a Poisson process.	Interarrival times in a queue, the time between phone calls
Poisson Distribution	Discrete numerical data representing the number of events occurring in a fixed interval.	Number of emails received per day, number of accidents per month
Geometric Distribution	Discrete numerical data representing the number of trials needed to achieve the first success.	Number of attempts to make a successful shot in basketball
Log-Normal Distribution	Continuous numerical data where the logarithm of the values follows a normal distribution.	Stock prices, incomes
Weibull Distribution	Continuous numerical data used to model reliability and failure rates.	Time to failure of a mechanical component
Gamma Distribution	Continuous numerical data used to model wait times, durations, and arrival rates.	Service times in a queue, time between arrivals in a Poisson process
Triangular Distribution	Continuous numerical data that is bounded and characterized by a peak at the mode.	Estimating project durations, uncertainty analysis

Things to Remember

Ensure your data is accurate and properly formatted. Incorrect or inconsistent data can lead to misleading distribution charts.
Choose the appropriate chart type for the distribution you want to visualize. Different types of charts are suited for different types of data.
Understand the underlying statistics and concepts related to the distribution you’re analyzing. This will help you interpret the chart accurately.
By default, you won’t get Data Analysis Toolpak add-in in your Excel ribbon. You have to add it.
If you input any non-numeric value while using the NORM.DIST function, you’ll get #VALUE! Error.

Frequently Asked Questions

1. How to do histogram Excel?

Excel provides the histogram chart type to display the distribution of your data. You can select your data, go to the “Insert” tab, choose the histogram chart type, and customize it to suit your needs.

2. How can I customize the appearance of my distribution chart in Excel?

You can modify the axes, add titles, adjust labels, change colors, and apply other formatting options to improve readability and visual appeal.

Download Practice Workbook

Distribution Chart.xlsx

<< Go Back to Excel Distribution Chart | Excel Charts | Learn Excel

Get FREE Advanced Excel Exercises with Solutions!