How to Calculate Eigenvectors in Excel (with Detailed Steps)

In linear algebra, when a set of equations forms a square matrix, we are able to form eigenvectors of that matrix. An eigenvector is a non-vector component that we derive from the scalar multiplication of the given square matrix.

The Eigenvector equation is:

Av=λv

A= Given a matrix of size n x n

v=Eigenvector

λ=Eigenvalue

The eigenvector is also known as the characteristic vector, and the eigenvalue is known as the characteristic value.

The calculation of an eigenvector is a complex and time-consuming process mathematically. In this article, we will explain the mathematical steps and apply the vector formula in Excel to solve them.

Step 1 – Insert Identity Matrix and Other Supporting Elements

First, we need to calculate the eigenvalues before we can calculate the eigenvectors. As detailed above, the mathematical expression of the eigenvector is:

Av=λv

or, Av-λv=0

or, v(A-λ)=0

Finally, v(A-λI)=0

As the A is a matrix, we need another matrix with the scalar λ. So we multiply λ by the Identity matrix. The Identity matrix will not change the value of the equation. In the calculation of eigenvalues, the determinant, det(A-λI) is considered to be 0.

Consider the following matrix:

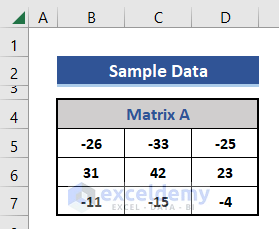
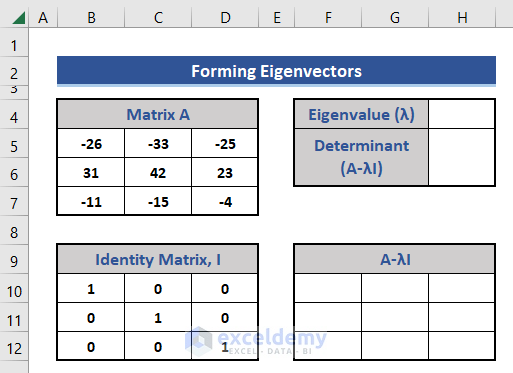
Insert an Identity Matrix, I of size 3×3 in the dataset.
Add other supporting components to the dataset.

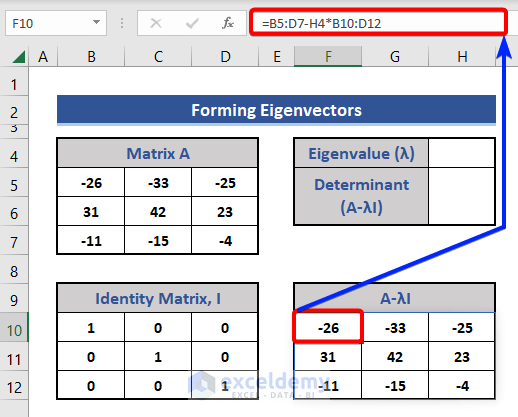
To find A-λI, enter this formula in Cell F10:

=B5:D7-I4*B10:D12

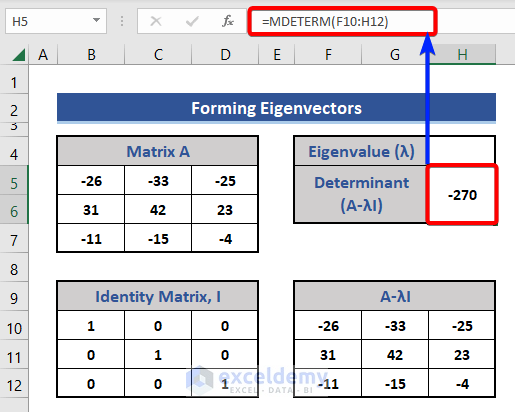
Step 2 – Calculate the Determinant Using the MDETERM Function

Excel has a default function, MDETERM, for calculating determinants.

To find the det(A-λI), enter the following formula in Cell H5:

=MDETERM(F10:H12)

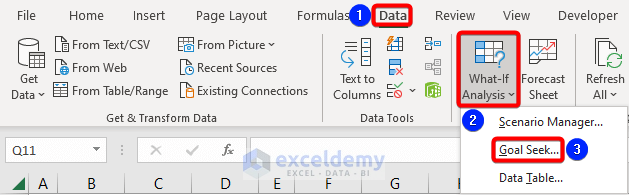
Step 3 – Enable Excel Goal Seek Feature

Now we can apply the Goal Seek feature to determine the eigenvalues.

Go to the Data tab,
Select What-If-Analysis from the Forecast group.
Select the Goal Seek option.

Step 4 – Calculate Eigenvalues

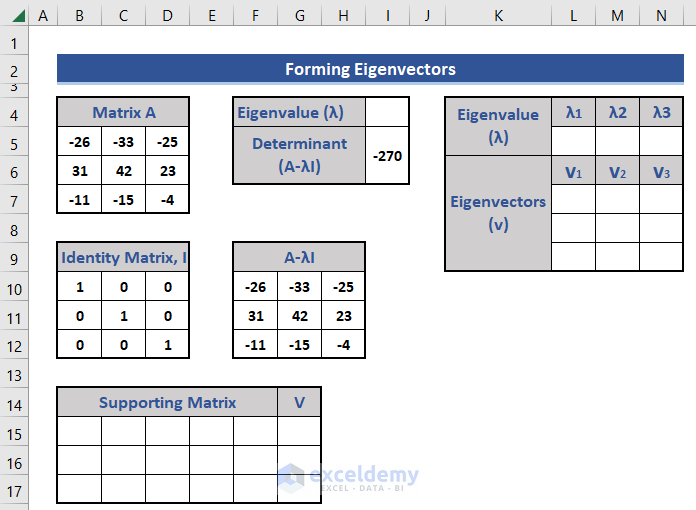
As the given matrix is 3×3, we will get 3 eigenvalues. And for each eigenvalue, we will get one eigenvector.

Add new cells in the dataset for 3 eigenvalues and eigenvectors.

The Goal Seek window appears by following Step 3.

Insert cell references for the two sections and set the determinant to zero (0) as in the following image.
Click OK.

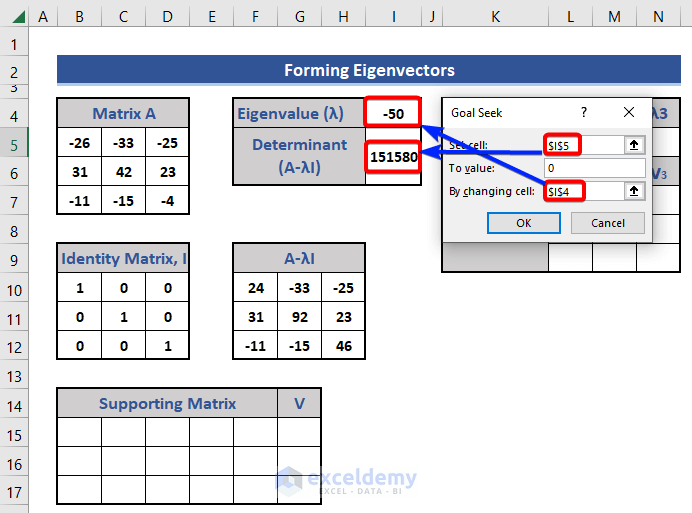
Here, the eigenvalue is the changing cell that we get by using the Goal Seek feature.

After processing, we see the optimized eigenvalue.

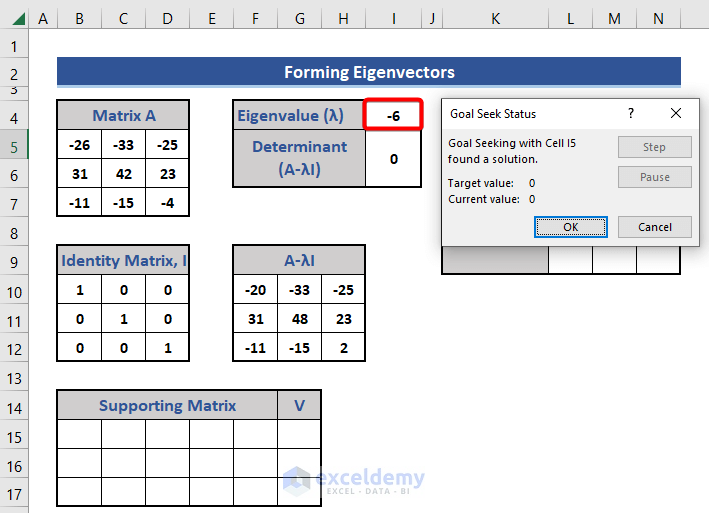
This is the 1st eigenvalue.

Copy Cell I4 by pressing Ctrl+C.
Paste this value in Cell L5 as λ1.
Select the Values option of the Paste Special section.

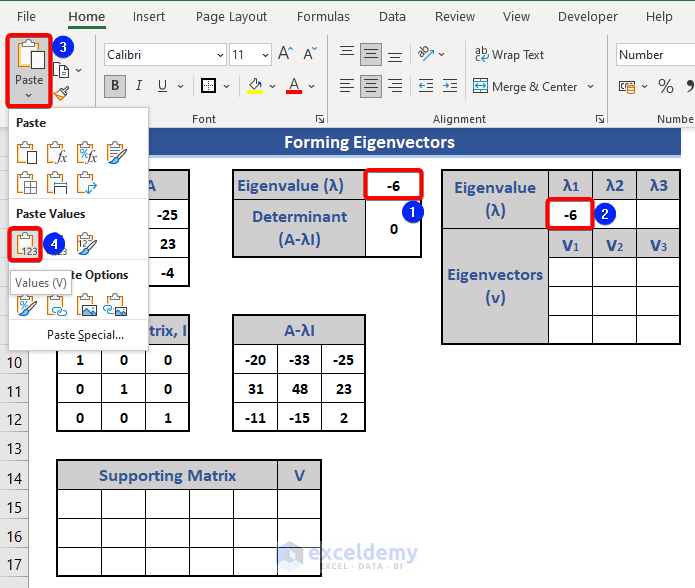
Step 5 – Find Eigenvectors for Each of the Eigenvalues

We already calculated the 1st eigenvalue. Now we can find the corresponding eigenvector.

Copy matrix A-λI by using the following equation in Cell B15:

=F10:H12

Copy the 1st and 2nd column of matrix A-λI in Cell E15 by using the following formula:

=F10:G12

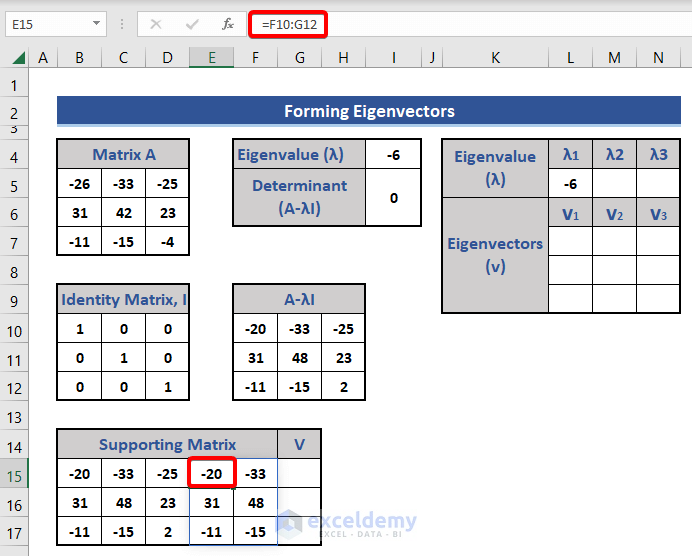
We get a 3×5 matrix. This will be used in the calculation of the eigenvectors. Each eigenvector must be a column matrix. As the given matrix is of size 3×3, the eigenvectors will be of size 3×1.

We use the MDETERM function to calculate the eigenvectors.

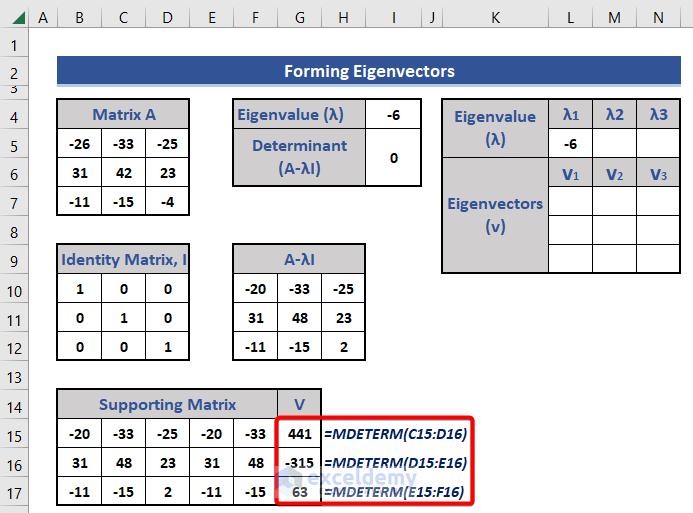
Insert the following formulas in Cells G15:G17:

In Cell G15:

=MDETERM(C15:D16)

In Cell G16:

=MDETERM(D15:E16)

In Cell G17:

=MDETERM(E15:F16)

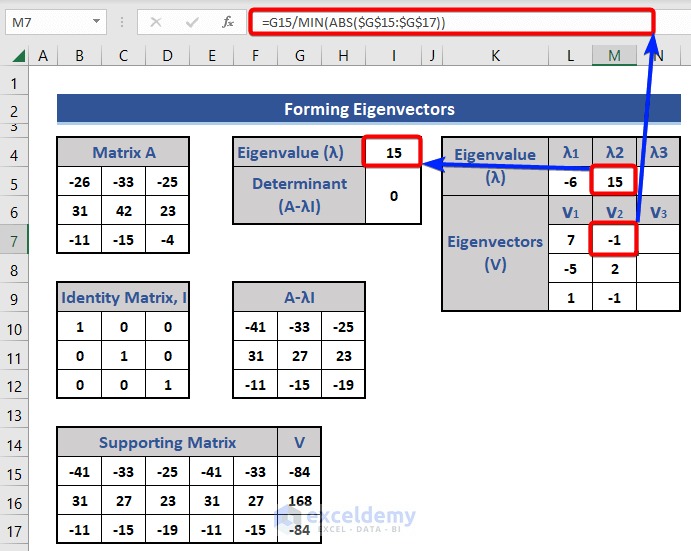
Optimize the eigenvector in Cell L7 by using the following formula:

=G15/MIN(ABS($G$15:$G$17))

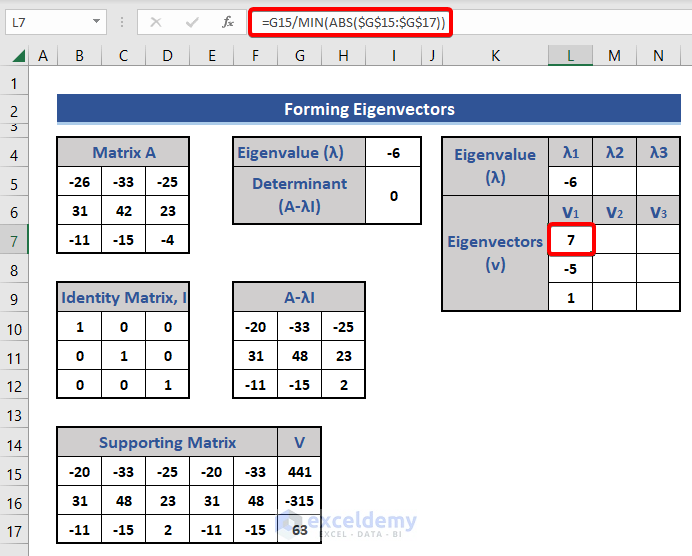
Use the paste-special technique described above to keep the values only.

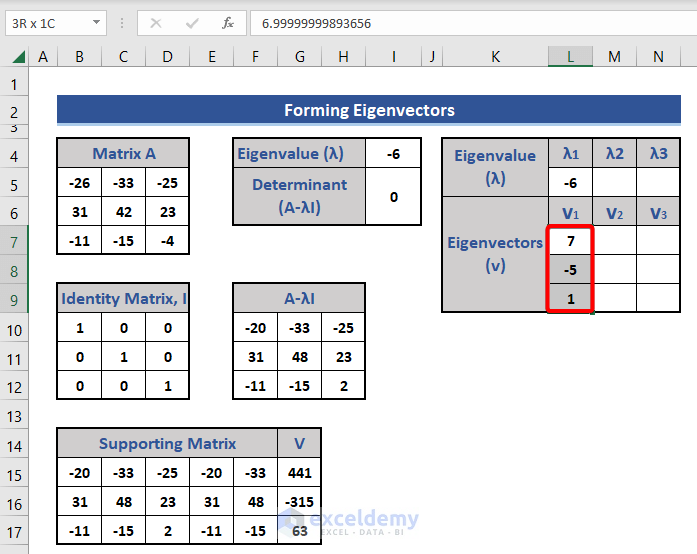
Step 6 – Calculate the Rest of the Eigenvalues and Eigenvectors

We will repeat Steps 4 and 5 again to get the rest of the eigenvalues and their corresponding eigenvectors.

Previously, we set the value of λ as negative. Now, set this a positive value and apply the Goal Seek feature.

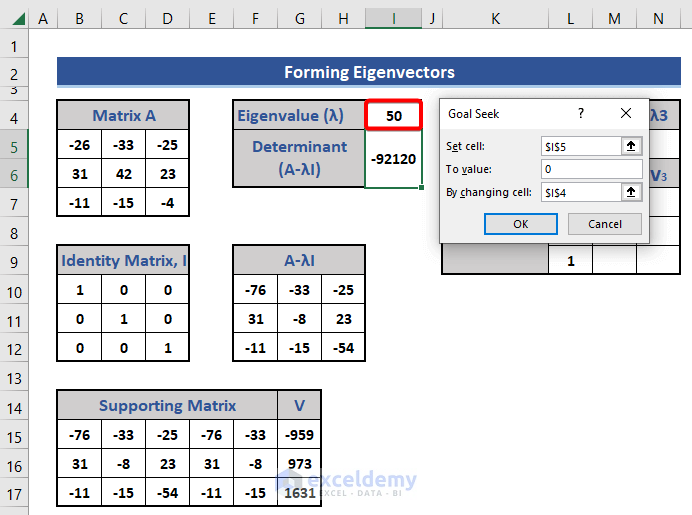
We get a new eigenvalue and eigenvector for that eigenvalue as shown before:

=G15/MIN(ABS($G$15:$G$17))

Set the eigenvalue to 0 and apply the Goal Seek feature again.

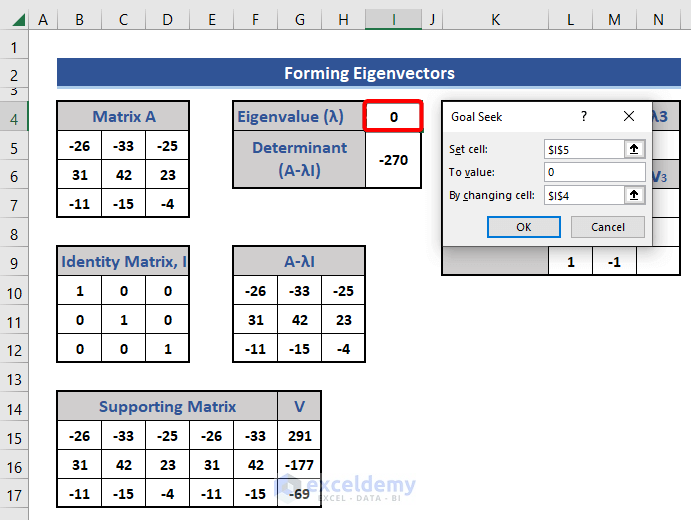
We get three eigenvalues and their corresponding eigenvectors.

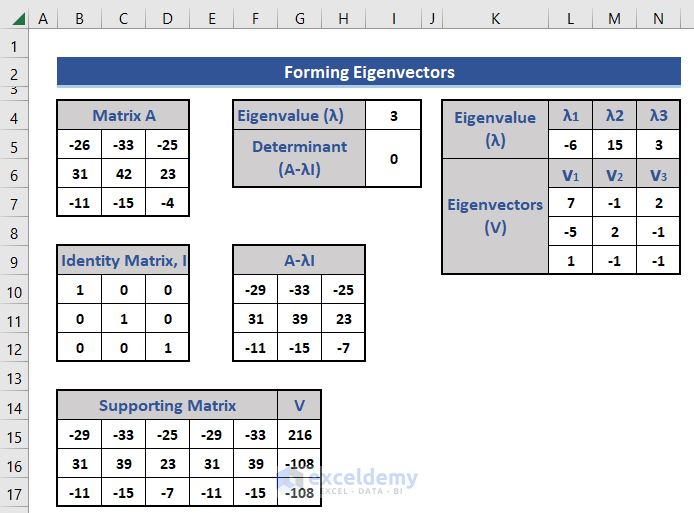
Ultimately we get V1, V2, and V3 as the 3 eigenvectors of three eigenvalues -6,15,3 respectively. All eigenvectors are column vectors.

Download Practice Workbook

Calculating Eigenvectors.xlsx

<< Go Back to | Vectors in Excel | Excel for Math | Learn Excel

Get FREE Advanced Excel Exercises with Solutions!

2 Comments

David Wood Dec 3, 2024 at 3:47 AM

I have it working for the 3 X3 matririx butI am trying to expand this to a 6×6 matrix. However, I am struggling with the codes and which determinates to calculate just in the final supporting matrix. Are you able to provide this?
Regards
- Reply
  Shamima Sultana Dec 3, 2024 at 10:17 AM
  Hello David Wood,
  
  To expand the method for eigenvectors to a 6×6 matrix in Excel:
  
  1. Set up the 6×6 matrix in Excel.
  2. Use Excel’s MMULT and MINVERSE functions to compute matrix operations.
  
  For determinants, you’ll need submatrices (e.g., 5×5) for characteristic polynomial calculation. Excel lacks a direct determinant function for larger matrices, so use VBA:
```
Function Determinant(M As Range) As Double
    Dim Matrix() As Double
    Dim n As Integer
    n = M.Rows.Count
    ReDim Matrix(1 To n, 1 To n)
    For i = 1 To n
        For j = 1 To n
            Matrix(i, j) = M.Cells(i, j).Value
        Next j
    Next i
    Determinant = Application.MDeterm(Matrix)
End Function
```
  Use this to calculate the determinant iteratively for the characteristic equation.
  
  Regards
  ExcelDemy