in this article, we’ll demonstrate 3 different examples of finding the Z Critical Value in Excel. The Z Critical Value plays a significant role in a Hypothesis Test. A Hypothesis Test generates a Test Statistic as the result, but to determine if this result is statistically significant or not, a comparison should be made between the Test Statistic and the Z Critical Value.
Introduction to the NORM.S.INV Function
The NORM.S.INV function in Excel determines the inverse of the standard normal cumulative distribution. The Mean is Zero and the Standard Deviation is 1 in the cumulative distribution.
- Syntax
=NORM.S.INV(probability)
- Arguments
probability: A probability corresponding to the standard normal cumulative distribution.
How to Find the Z Critical Value in Excel: 3 Suitable Examples
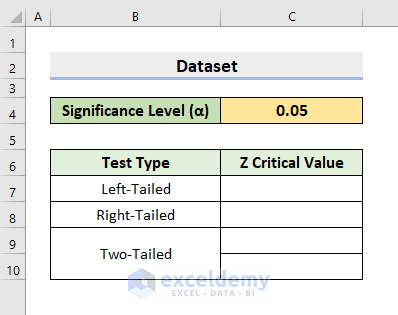
For hypothesis test results to be considered statistically significant, the absolute value of the test statistic needs to be greater than the Z critical value. To illustrate, we’ll use the below dataset where the Significance Level (α) is 0.05 and compute the Z critical value for 3 different test types.
Example 1 – Calculate the Z Critical Value in a Left-Tailed Test
Let’s find the critical value by applying the Significance Level (α) as a probability in the argument of the NORM.S.INV function.
Steps:
- Select cell C7.
- Enter the following formula:
=NORM.S.INV(C4)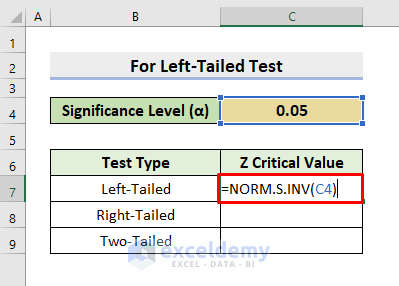
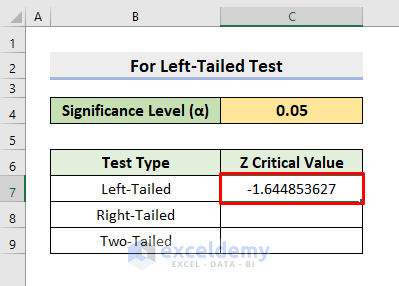
- Press Enter to return the value.
The desired result is returned.
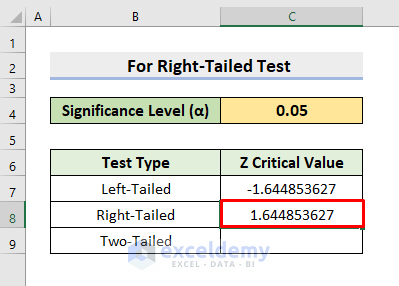
Example 2 – Find the Z Critical Value in a Right-Tailed Test
As in the case of a left-tailed test, one critical value is also returned as output of a Right-Tailed test. In a right-tailed test case, we need to subtract the Significance Level from 1, so we’ll modify the Significance Level (α) to insert it in the argument of the NORM.S.INV function.
STEPS:
- Select cell C8.
- Insert the below formula:
=NORM.S.INV(1-C4)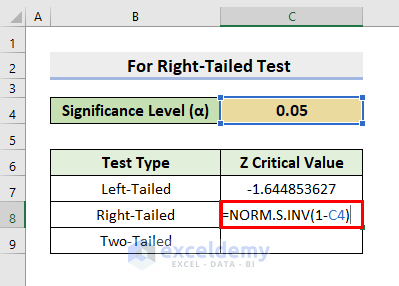
- Return the result by pressing Enter.
The Z critical value for the right-tailed test is returned.
Read More: How to Find T Critical Value in Excel
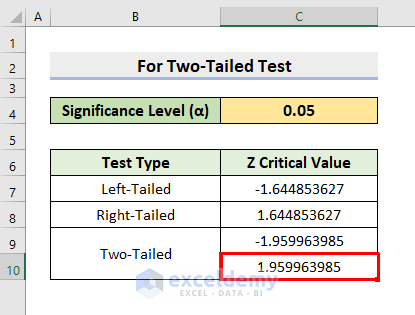
Example 3 – Determine the Z Critical Value for a Two-Tailed Test
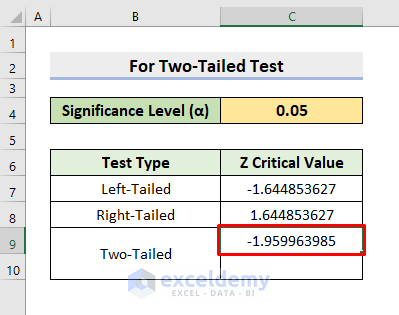
A Two-Tailed test returns 2 critical values as output. We’ll input the Significance Level (α) as a probability in the argument of the NORM.S.INV function, but we’ll have to edit it first. As it’s two-tailed, we’ll divide the Significance Level by 2 to get one critical value. Then, to find the second critical value, we’ll subtract the division output from 1.
STEPS:
- Click on cell C9.
- Enter the formula below:
=NORM.S.INV(C4/2)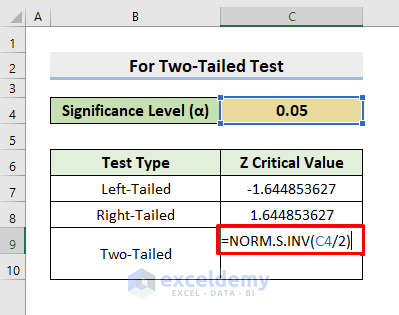
- Press Enter to return the result.
- To find the second critical value, select cell C10.
- Enter the formula below:
=NORM.S.INV(1-C4/2) 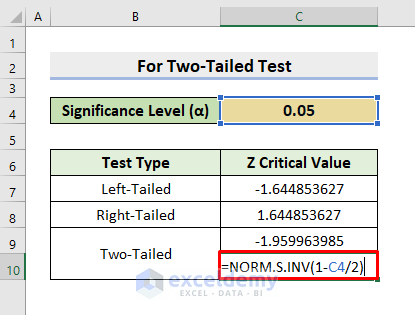
- Press Enter.
The two critical values for the two-tailed test are returned.
Download Practice Workbook
Related Article
<< Go Back to Critical Value in Excel | Excel for Statistics | Learn Excel
Get FREE Advanced Excel Exercises with Solutions!

