Formulas for Horizontal Cylindrical Tank Volume Calculator
The volume of a cylinder can be of two types: fully and partially filled. Partially filled volume can also be of two types during calculation: filled less than 50% or more than 50%.
- Formula for Volume of a Fully Filled Tank:
V = πR2L
Here,
R = Radius of the cylinder base
L = Length of the cylinder’s horizontal axis
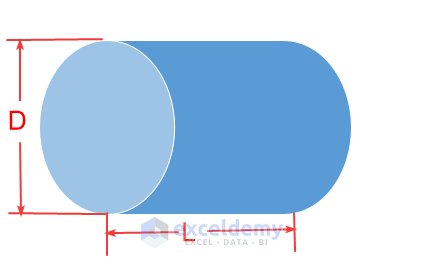
- Formulas to Calculate Volume of a Partially Filled Tank:
Filled Less Than 50% (F<R)
Segment Height (S) = Filled Height (F)
Segment Area = ((R2cos-1(1-S/R)-(R-S)×√(2RS-S2))
Volume (V) = Length × Segment Area = L ×((R2cos-1(1-S/R)-(R-S)×√(2RS-S2))
Here,
R = Radius
S = Segment Height
L = length
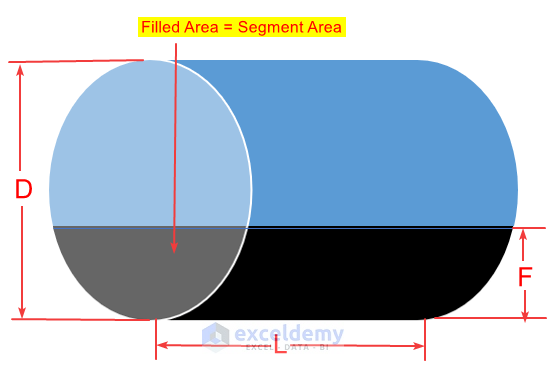
Segment Area:
In the figure, the black part is the segment area. When the filled height (F) is less than Radius(R), the segment area is equal to the filled area. And when the filling height is greater than the Radius(R), the segment area will be the remaining unfilled part of the cylinder.
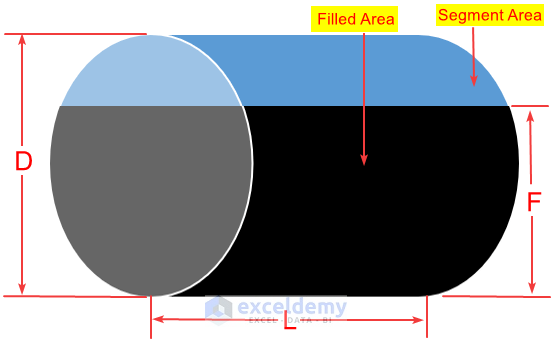
Filled More Than 50% (F>R)
Segment Height (S) = Diameter(D) – Filled Height (F)
Segment Area = ((R2cos-1(1-S/R)-(R-S)×√(2RS-S2))
Volume (V) =Full volume – Length × Segment Area = πR2L – L ×((R2cos-1(1-S/R)-(R-S)×√(2RS-S2))
Horizontal Cylindrical Tank Volume Calculator in Excel: 2 Examples
To compute the volume of the cylindrical tank, we have to convert all the units to S.I. units to get the volume in m3 units. We can use other units instead, but here we’ll use S.I. units. To use other units, at the bottom of this article is a handy measurement unit conversion calculator.
Example 1 – Volume Calculator for Fully Filled Horizontal Cylindrical Tanks
Assume we have all the units converted to S.I units. Now we can calculate the full volume of a cylinder tank.
Steps:
- Enter the value of the length and diameter in cells C5 and C6 respectively.
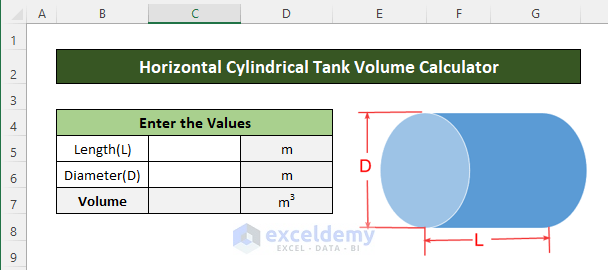
- Enter the following formula in cell C7 to calculate the full volume of the cylinder:
=PI()*(C6/2)^2*C5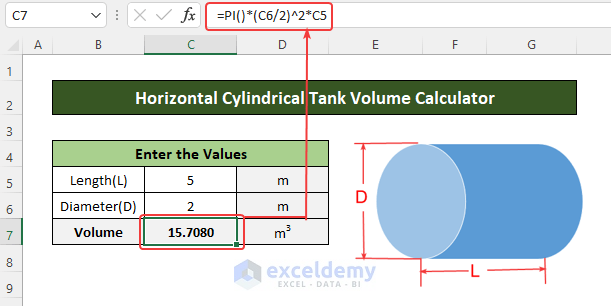
Method 2 – Volume Calculator for Partially Filled Horizontal Cylindrical Tanks
When a tank is partially filled, there may be two circumstances: either it is filled to less than half of its capacity, or it is filled to more than half its volume. For these two situations, the volume has to be calculated differently.
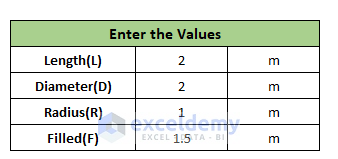
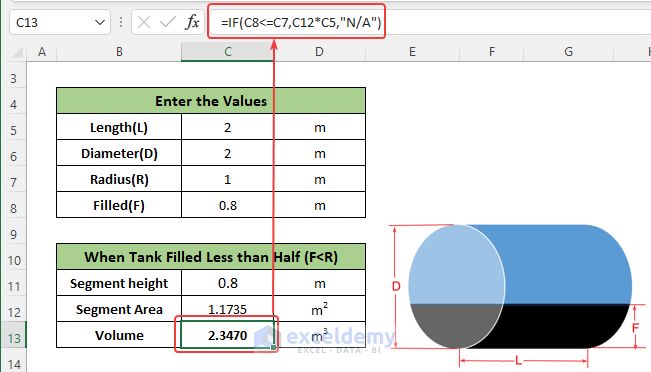
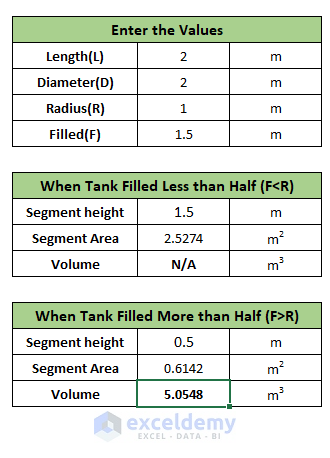
When Tank Is Filled Less Than 50% (F<R):
Steps:
- Enter the value of length, radius, and the filled height of the cylinder.
- Enter the following formula in cell C11 to calculate the segment height, which is equal to the filled height when F<R:
=C8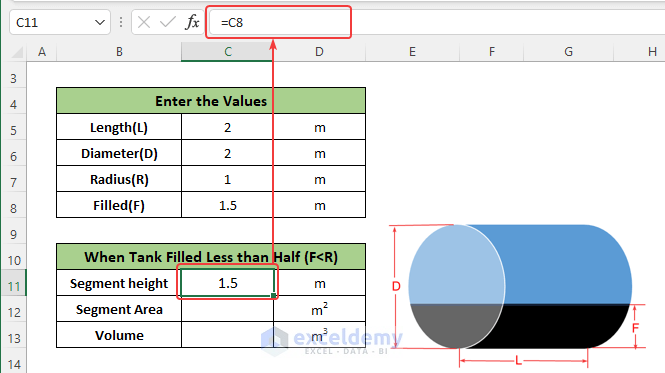
- Enter the following formula in cell C12 to calculate the segment area:
=($C$7^2)*ACOS(1-C11/$C$7)-($C$7-C11)*SQRT(2*$C$7*C11-C11^2)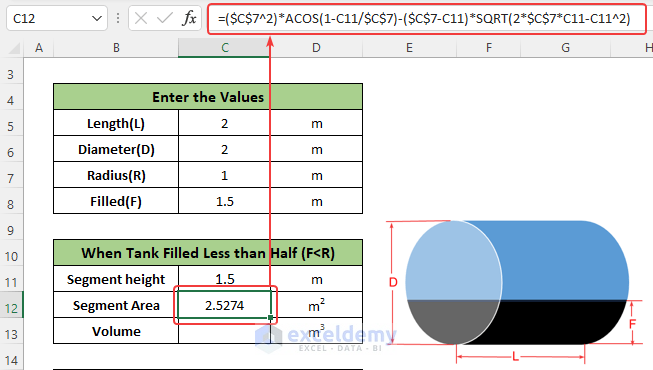
- Enter the following formula in cell C13 to calculate the partially filled volume:
=IF(C8<=C7,C12*C5,"N/A")The If function will return a result when the filled height is less than the radius, otherwise it will return “N/A”
When Tank Is Filled More Than 50% (F>R):
If the cylindrical tank filled to more than the half volume, we subtract the segment volume from the full volume. The segment height will be the difference between the filled height and the full height.
Steps:
- Enter the following formula in cell C16:
=C6-C8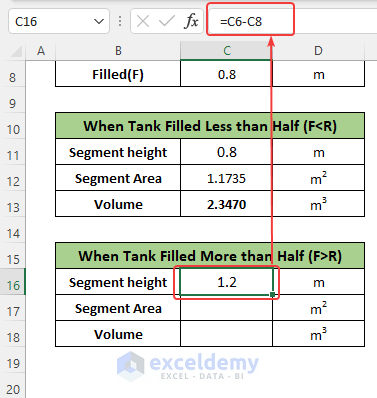
- Use a similar formula to calculate the segment area in cell C17:
=($C$7^2)*ACOS(1-C16/$C$7)-($C$7-C16)*SQRT(2*$C$7*C16-C16^2)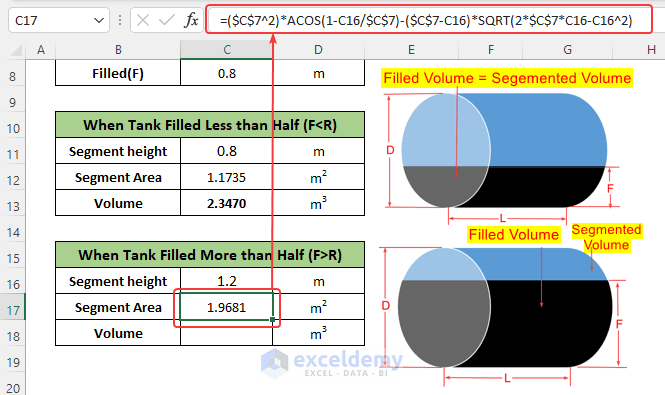
- The partially filled volume will be the subtraction of segment volume from the full volume. To calculate this, enter the following formula in cell C18:
=IF(C8>C7,PI()*C7^2*C5-C17*C5,"N/A")- The If function returns a result when the filled height is higher than the radius, otherwise it returns “N/A”
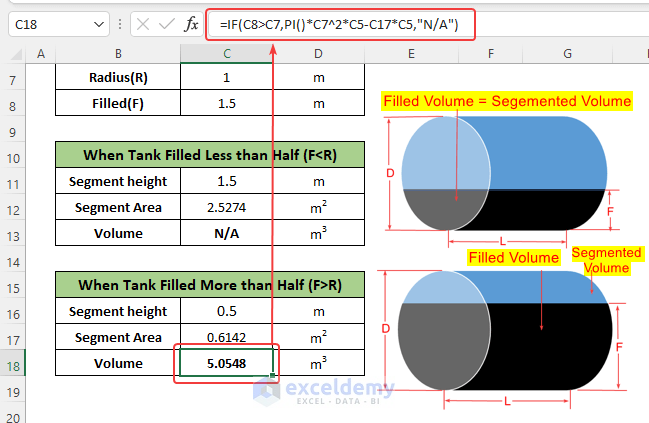
The calculator is ready to use.
Things to Remember
During the calculation of the volume of a cylinder or any other thing, you must use constant units. If you have values in any other kind of unit, you must convert the measurement units to the specific constant unit required. To assist you with this process, included in the downloadable sample workbook below is a free Measurement Unit Converter that can convert between different unit types.
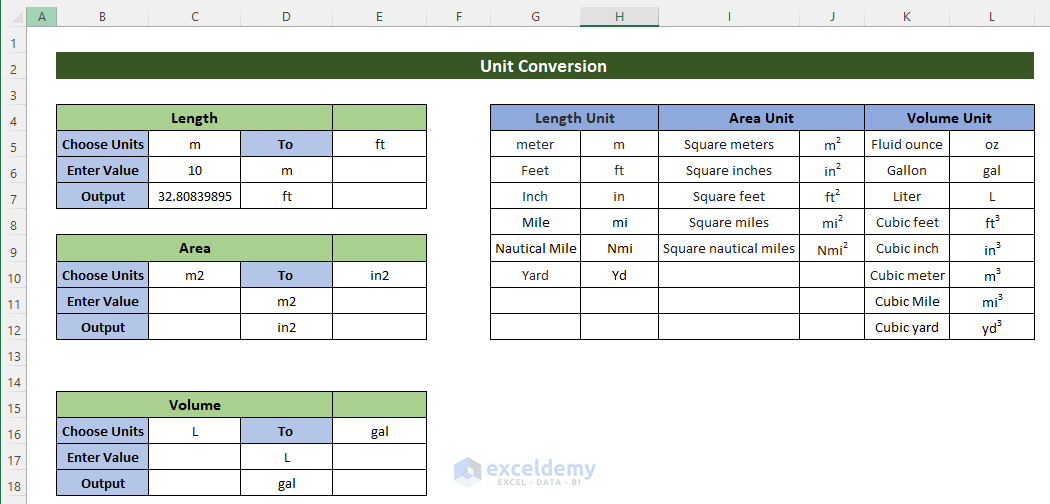
There is a drop-down option in each cell where you can select which units to convert to and from.
Download Sample Workbook
<< Go Back to Excel Area & Volume Calculator | Excel Templates
Get FREE Advanced Excel Exercises with Solutions!


If possible, pl. send HT tank with dish calculation for each cm (1 cm to 200cm)for 15KL, Length-500cm, Diameter:200cm
Hello A.Nirmala Rani,
You can the following formula for the volume of a cylindrical segment:

Where:
V is the volume in liters,
L is the length of the cylinder in meters,
R is the radius of the cylinder in meters,
h is the height of the liquid level in meters.
Given the specific dimensions:
L=5.0 meters (500 cm),
R=1.0 meter (100 cm),
h varies from 0.01 meters (1 cm) to 2.0 meters (200 cm)
This formula calculates the volume of the liquid based on the height from the base up to the liquid level within a horizontal cylindrical tank. To use this formula, ensure to convert all measurements (radius, length, and height) to meters before applying them in the calculation.
At 1 cm height: Approximately 9.41 liters
At 2 cm height: Approximately 26.59 liters
At 3 cm height: Approximately 48.77 liters
At 4 cm height: Approximately 74.97 liters
At 5 cm height: Approximately 104.62 liters
At 10 cm height: Approximately 293.63 liters
———————————————————
To see the full list of calculated volumes for each centimeter increment from 1 cm to 100 cm for the horizontal cylindrical tank, Download the Excel File.
List of Calculated Volumes.xlsx
Regards
ExcelDemy