The Capital Asset Pricing Model (CAPM) is a widely-used financial model for estimating the expected return on an asset. In an article, we will show how to calculate CAPM beta in Excel. In the methods, we will use Excel formulas, different Excel options, and VBA code.
Check out the overview image for the procedure to calculate CAPM Beta.
What Is Capital Market Pricing Model (CAPM)?
One of the key inputs for the model is the asset’s Beta, which measures its systematic risk. Excel is a useful tool for calculating beta. The Capital Asset Pricing Model (CAPM) is a financial model that helps investors and financial analysts to determine the expected return on an asset or capital based on its risk and the risk-free rate of return. It assumes that investors are risk-averse and require compensation for taking on additional risk beyond the risk-free rate of return. The model estimates the expected return of an asset by taking into account the asset’s beta (systematic risk) and the expected market risk. CAPM is widely used in finance to determine the cost of capital for investments and to evaluate the performance of investment portfolios.
What Is CAPM Beta?
Beta is an important measure used in finance to evaluate the performance of an investment compared to its standard.
Beta measures how much an investment’s returns move in response to changes in the standard returns. A beta of 1 indicates that an investment’s returns move in line with the standard returns, while a beta greater than 1 indicates that the investment is more volatile than the standard, and a beta less than 1 indicates that the investment is less volatile than the standard. The formula to calculate Beta is-
Beta = Covariance of the portfolio returns with the expected returns / Variance of the portfolio returns
How to Calculate CAPM Beta in Excel: 3 Quick Methods
In this section, we will discuss three different methods to determine Beta in Excel. We will use Excel formulas, the Data Analysis ToolPak, and VBA code to do the job. Without any further delay, let’s move on to the procedures.
1. Calculating CAPM Beta Using Excel Formula
In the first method, we will use the COVARIANCE.P and VAR.P functions of Excel to calculate CAPM beta. Let’s follow the given instructions.
- Firstly, prepare a dataset containing Portfolio Returns (standard returns) and Market Returns data.
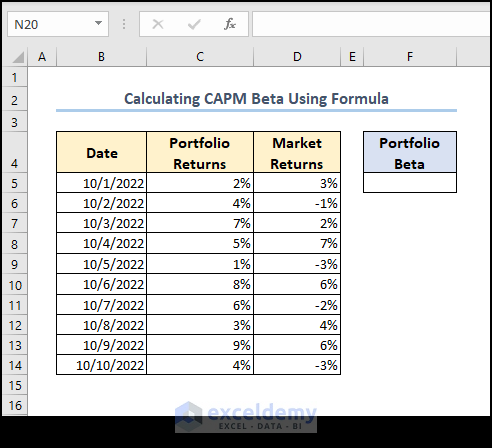
- Then, apply the following formula to Portfolio Beta (CAPM Beta).
=COVARIANCE.P(C5:C14,D5:D14)/VAR.P(C5:C14)
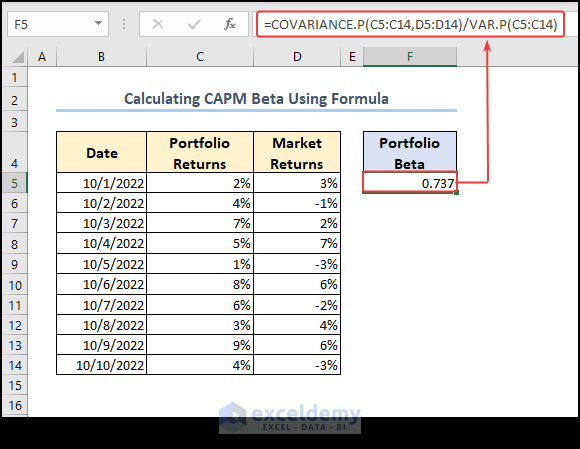
In the formula, we calculate the covariance of data from ranges C5:C14 and D5:D14 with the COVARIANCE.P function. Then, we determined the variance of data from range C5:C14 with the VAR.P function and divided the covariance output by the variance output to obtain the CAPM beta.
Read More: How to Calculate Alpha and Beta in Excel
2. Applying Analysis ToolPak to Calculate CAPM Beta
Excel has many built-in options; we will use the Data Analysis ToolPak to calculate the CAPM Beta. This time we won’t use any formulas.
- Firstly, select the Data tab > Data Analysis.
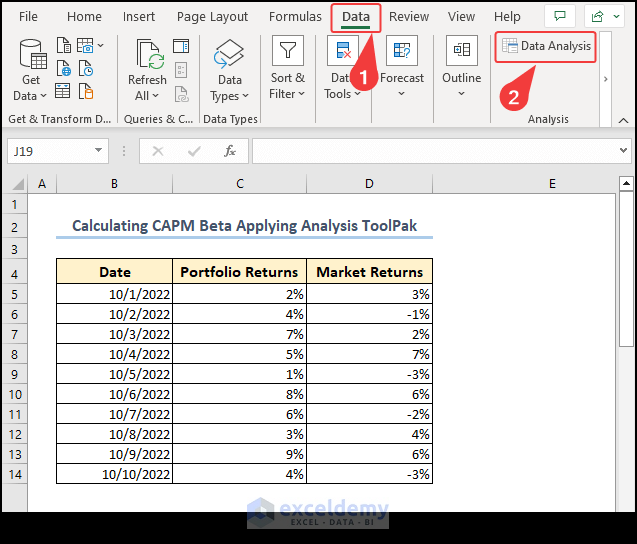
- Afterward, select Regression option from the Data Analysis tab.
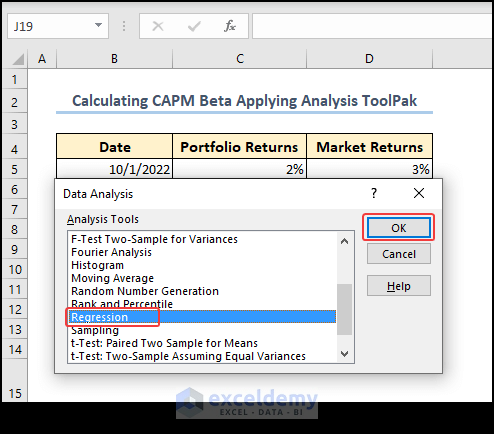
- Then, from the Regression tab, enter the reference range for data of Portfolio Returns and Market Returns in the Input Y Range and Input X Range sections respectively. Also, select the range for output in the Output Range section.
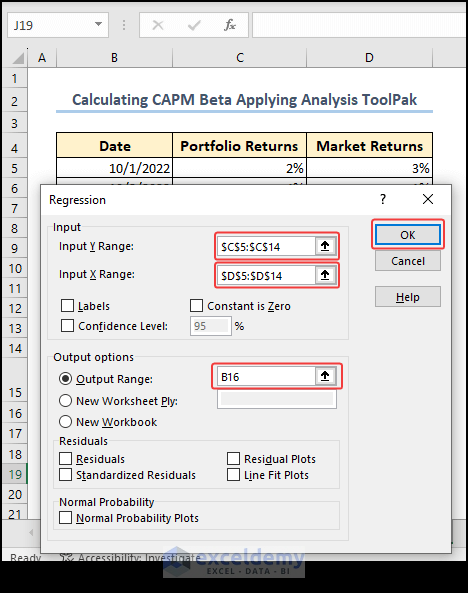
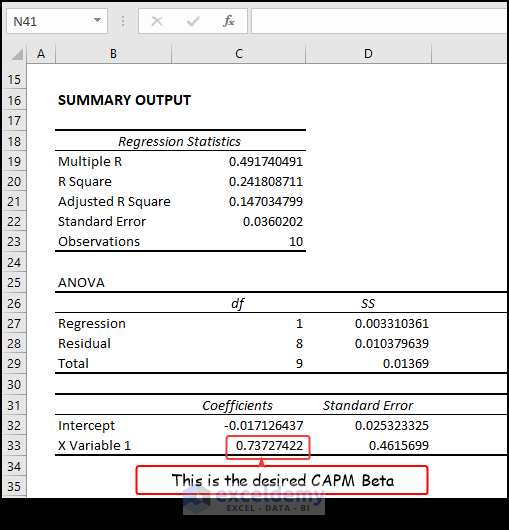
- Lastly, after pressing OK, you will see the various analysis results in the worksheet. CAPM Beta is one of them.
Read More: How to Calculate the Alpha of a Stock in Excel
3. Use of Excel VBA to Calculate CAPM Beta
As we know, almost every task in Excel can be done with VBA. Now, we will show you how to calculate beta with the help of VBA.
- Firstly, open the VBA window by pressing Alt + F11. You can also select the Developer tab > Visual Basic.
- Afterward, select Insert > Module to open a new code module.
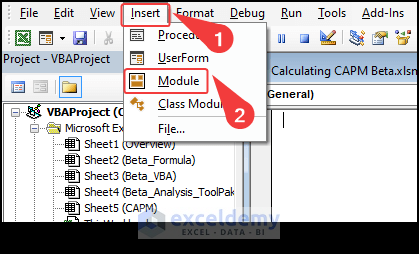
- Next, use the attached code in the module and run it.
Code:
Sub Beta_VBA()
Dim P_Returns As Range
Dim M_Returns As Range
Dim Covariance As Double
Dim Variance As Double
Dim Beta As Double
Set P_Returns = Worksheets("Beta_VBA").Range("C5:C14")
Set M_Returns = Worksheets("Beta_VBA").Range("D5:D14")
Covariance = WorksheetFunction.Covariance_P(P_Returns, M_Returns)
Variance = WorksheetFunction.Var_P(P_Returns)
Beta = Covariance / Variance
Worksheets("Beta_VBA").Range("F5") = Beta
End Sub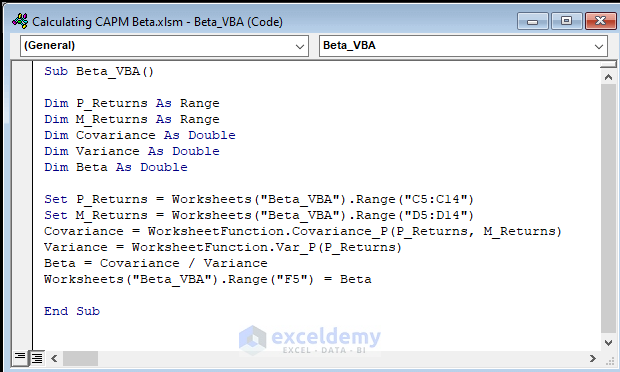
- As a result, you will the find the CAPM Beta in the worksheet.
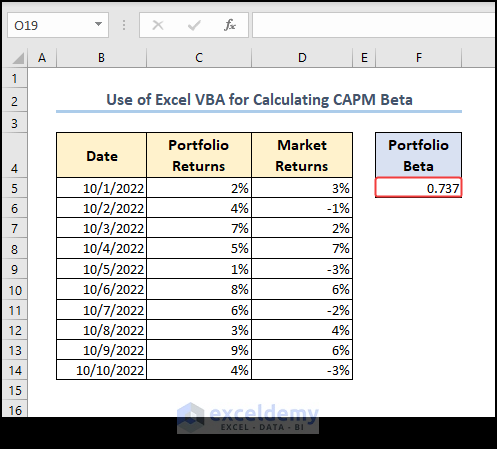
Code Breakdown:
- Firstly, we declared a sub-procedure and defined some necessary variables.
- We defined two ranges P_Returns and M_Returns as input ranges.
- Later on, we used the VBA Covariance_P function to get the covariance of data from ranges C5:C14 and D5:D14. We also used the VBA Var_P to get the variance of data from range C5:C14.
- Lastly, we divided the covariance result by the variance result to get beta. Also, we printed the result in the worksheet.
Read More: How to Calculate Alpha in Excel
How to Use CAPM Beta to Get Expected Return
In this segment, we will discuss the use of the CAPM model to determine Expected Return which will take Risk-Free Rate into account. Let’s move on to the procedure.
Here, we will use the following CAPM formula-
r = Rf + β * (Rm - Rf)
where,
- r is expected return
- Rf is the risk-free rate
- β is the capm beta
- Rm is the expected market return (average).
Now follow the steps to get Expected Return.
- Firstly, we need to determine the average of the data from Market Returns. Use the following formula for that.
=AVERAGE(D5:D14)
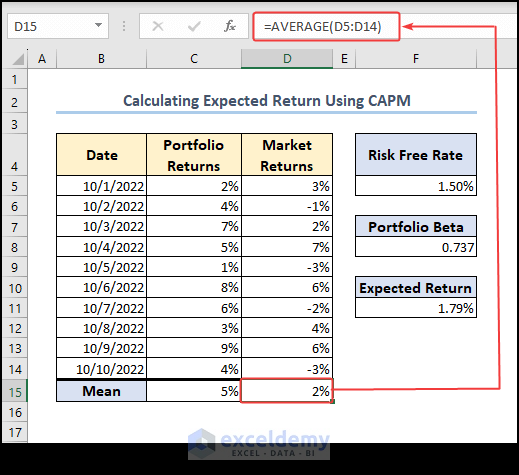
In the formula, the AVERAGE function finds the average of data from the range D5:D14.
- Define a Risk-Free Rate for the calculation. We have taken 1.5% as a risk-free rate.
- Next, calculate the beta as we did before.
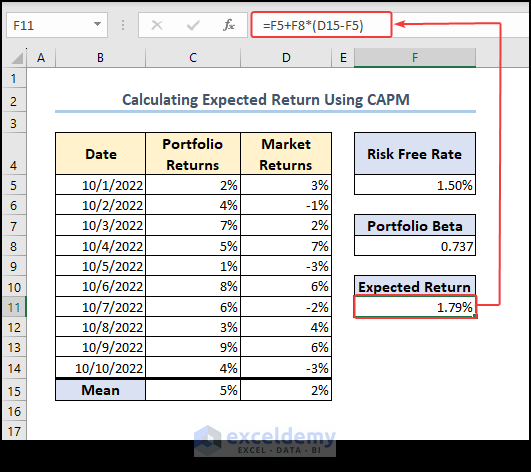
- Lastly, apply the following formula in a cell to calculate the Expected Return there.
=F5+F8*(D15-F5)
Here, F5, F8, and D15 cells are risk-free rate, portfolio beta, and average market returns respectively.
Frequently Asked Questions
- How do we interpret beta values?
Ans: A beta of 1 indicates that an investment’s returns move in line with the standard returns, while a beta greater than 1 indicates that the investment is more volatile than the standard, and a beta less than 1 indicates that the investment is less volatile than the standard.
- Can beta change over time?
Ans: Yes, beta can change over time due to changes in market conditions, company performance, and other factors. Investors should regularly reassess their holdings and adjust their portfolios as necessary to maintain their desired level of risk.
Things to Remember
- Be careful while dealing with cell references in the formula. In some cases, we used absolute cell references with the “$” sign.
- Change the Risk-Free Rate according to your needs.
- Don’t forget to save the file as an .xlsm file before running the macro.
Download Practice Workbook
Conclusion
As we discussed, the capm beta is a very useful tool for business analysis. Here, we have shown different methods to calculate capm beta in Excel. Hope, it’ll come in handy for you. Please leave a comment if you have queries or suggestions.
