What Is Logistic Regression?
Logistic regression analysis is a statistical learning algorithm that predicts the value of a dependent variable based on some independent criteria. It comes in three types:
Binary Logistic Regression: In the binary regression analysis model, we define a category by only two cases such as Yes/No or Positive/Negative.
Multinomial Logistic Regression: Multinomial logistic analysis works with three or more classifications. If we have more than two classified sections to categorize our data, we can use this regression analysis model.
Ordinal Logistic Regression: This regression analysis model works for more than two categories. However, in this model, we need a predetermined order to categorize them.
How to Do Logistic Regression in Excel: with Quick Steps
We will perform the binary logistical regression analysis. This type of analysis provides us with a prediction value of the desired variable.
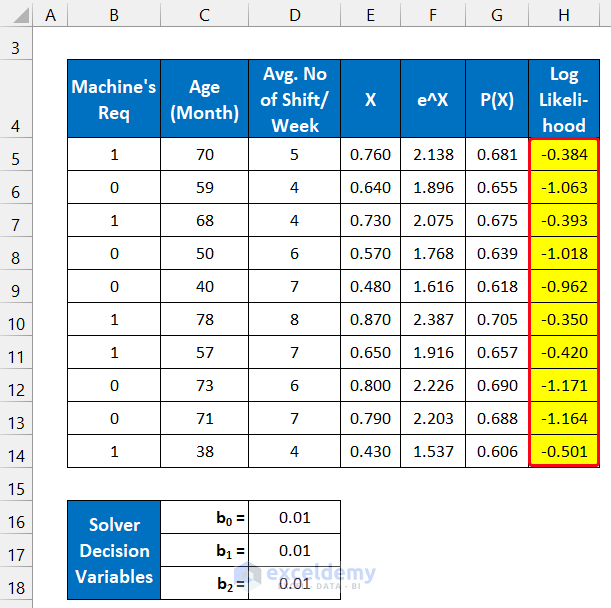
We’ll consider a dataset of 10 machines from an industry. The machine’s availability uses two states: 1=positive, 0=negative, and these values are shown in column B. The ages of those machines are in column C and the average duty hours per week is in column D. The initial regression solver variables are in the range of cells C16:D18.
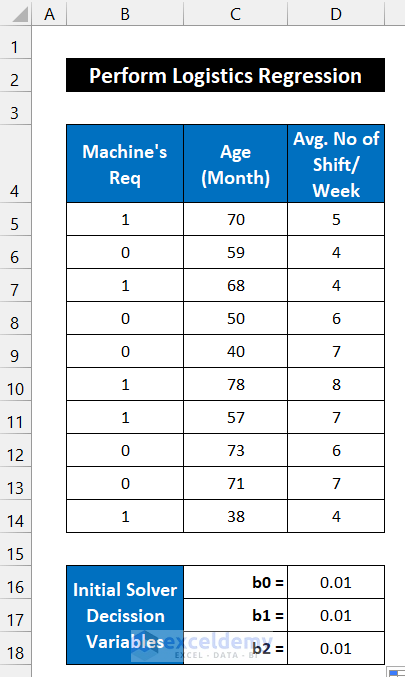
Step 1 – Input Your Dataset
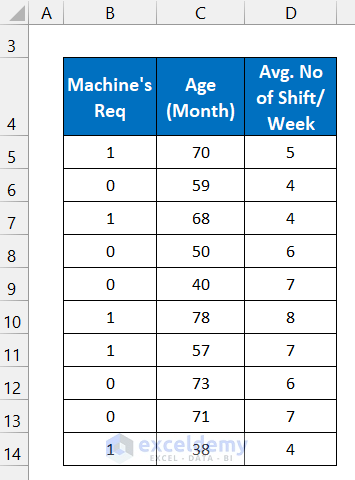
- Input your dataset accurately into Excel. We input the dataset in the range of cells B5:D14.
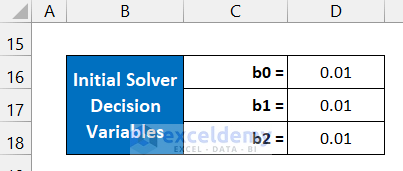
- Input the Solver Decision Variables in the range of cells D16:D18.
- We are assuming all the values as 0.01.
Step 2 – Evaluate the Logit Value
We define the Logit value as X in our calculation. The formula for the Logit value is:
![]()
b0, b1, and b2 are regression variables.
- Use the following formula in cell E5:
=$D$16+$D$17*C5+$D$18*D5
- Press the Enter key on your keyboard.
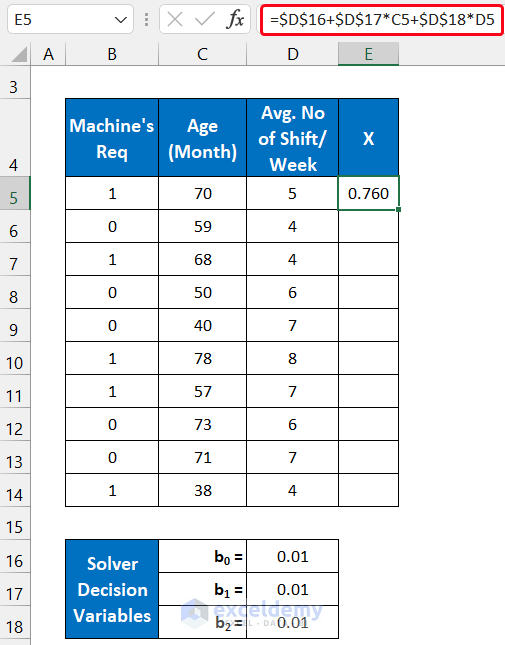
- Double-click on the Fill Handle icon to copy the formula down to cell E14.
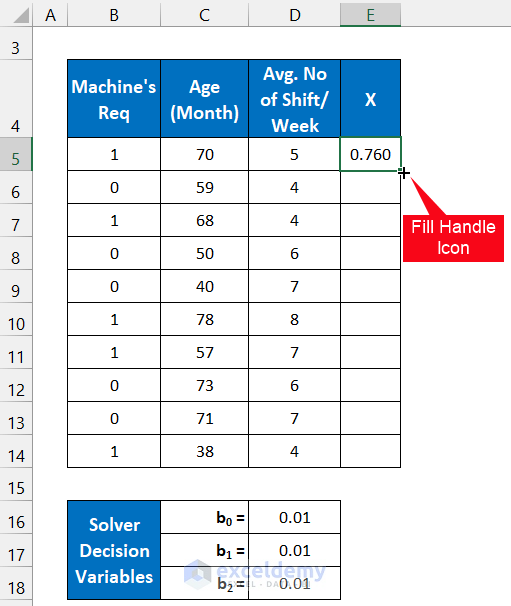
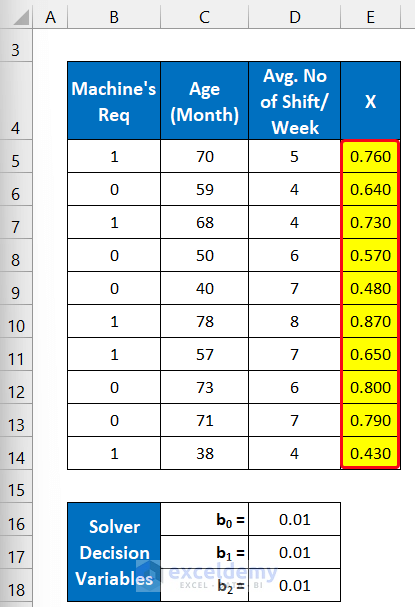
- You will get all the values of X.
Step 3 – Determine the Exponential of Logit for Each Data Point
- Use the following formula in cell F5:
=EXP(E5)
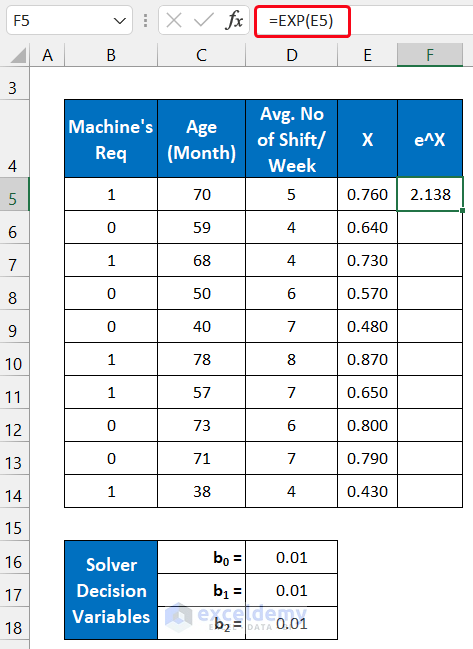
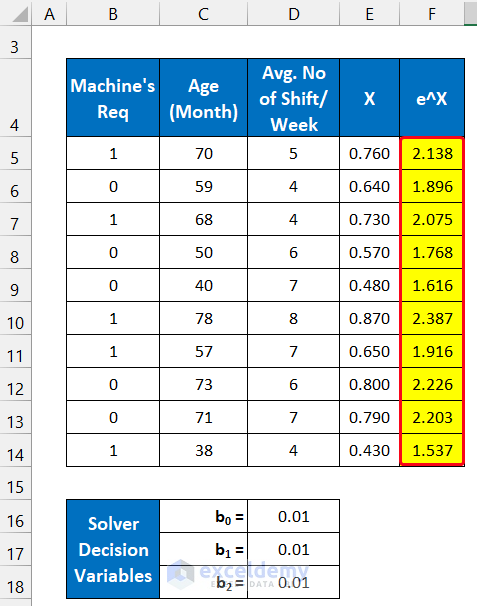
- Double-click on the Fill Handle icon to copy the formula.
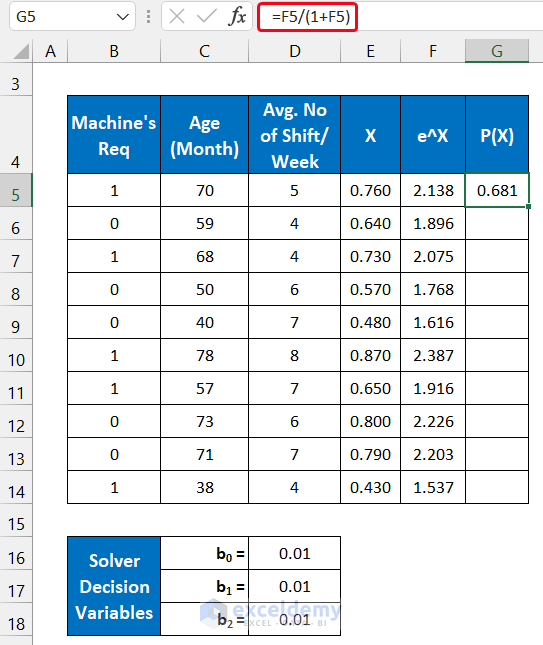
Step 4 – Calculate the Probability Value
P(X) is the probability value for occurring the X event.
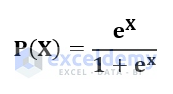
- Use the following formula in cell G5.
=F5/(1+F5)
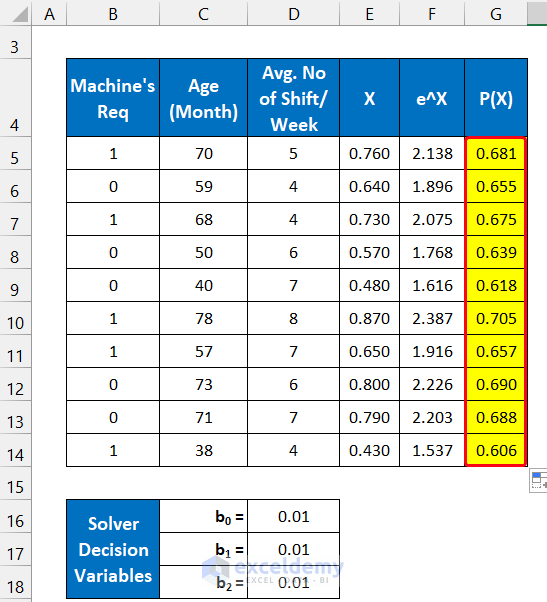
- Press the Enter key.
- Drag the Fill Handle icon down to G14 to get the results.
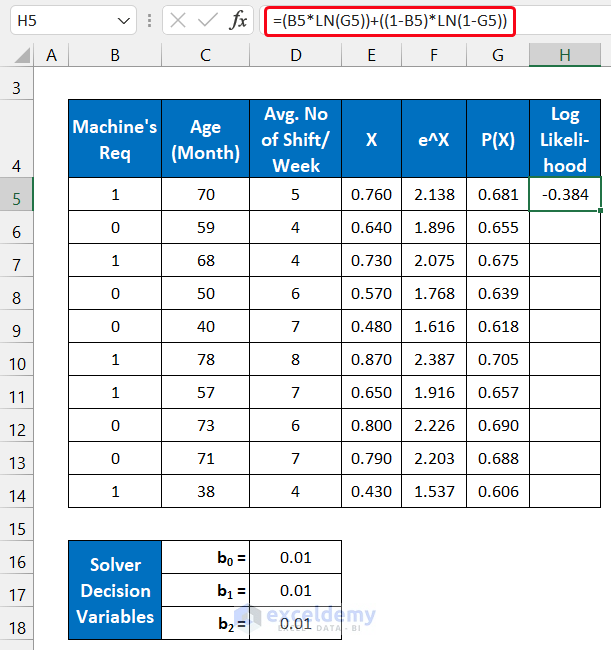
Step 5 – Evaluate the Sum of Log-Likelihood Value
- In cell H5, insert the following formula:
=(B5*LN(G5))+((1-B5)*LN(1-G5))
- Press the Enter key on the keyboard.
- Double-click on the Fill Handle icon to determine all log-likelihood values.
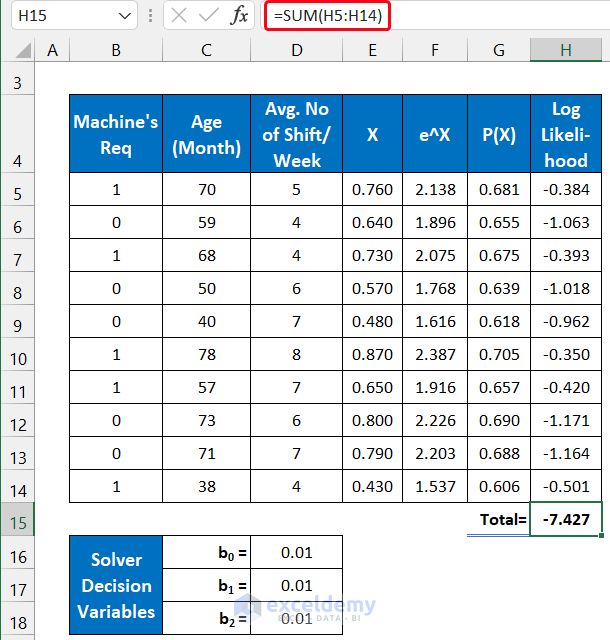
- In cell H15, use the following formula to sum all the values.
=SUM(H5:H14)
Breakdown of the Formula
We are doing this breakdown for cell H5.
LN(G5): This function returns -0.384.
LN(1-G5): This function returns -1.144.
(B5*LN(G5))+((1-B5)*LN(1-G5)): This function returns -0.384.
Step 6 – Use the Solver Analysis Tool for Final Analysis
- Select File and go to Options.
- A dialog box called Excel Options will appear.
- Select the Add-ins option.
- Choose the Excel Add-ins option in the Manage section and click Go.
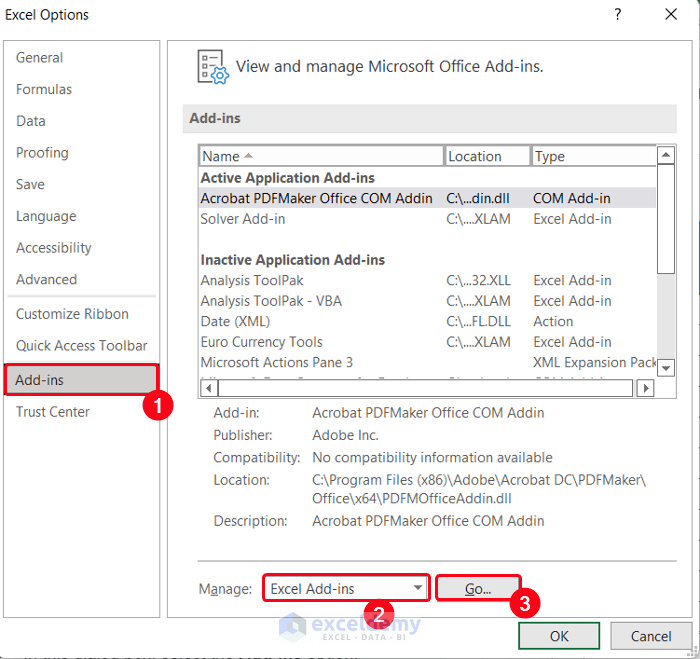
- A small dialog box titled Add-ins will appear.
- Check the Solver Add-in option and click OK.
- Close Excel Options.
- Go to the Data tab, and you will find the Solver command in the Analysis group.
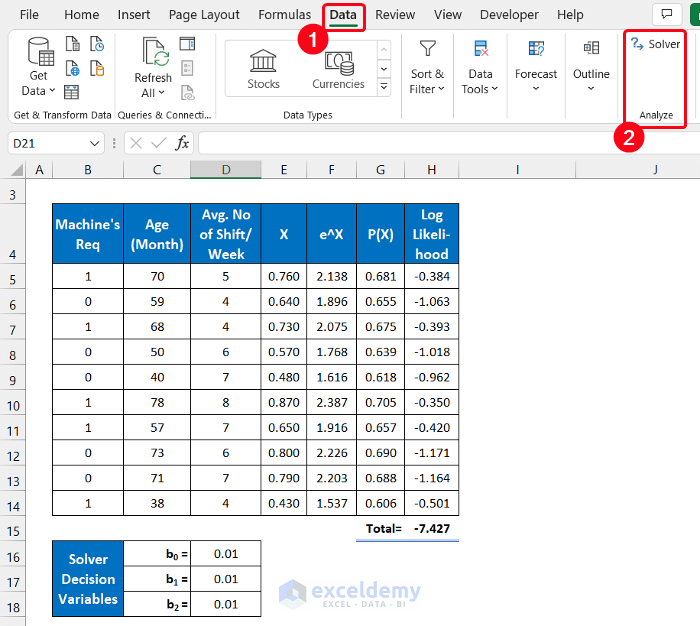
- Click the Solver command.
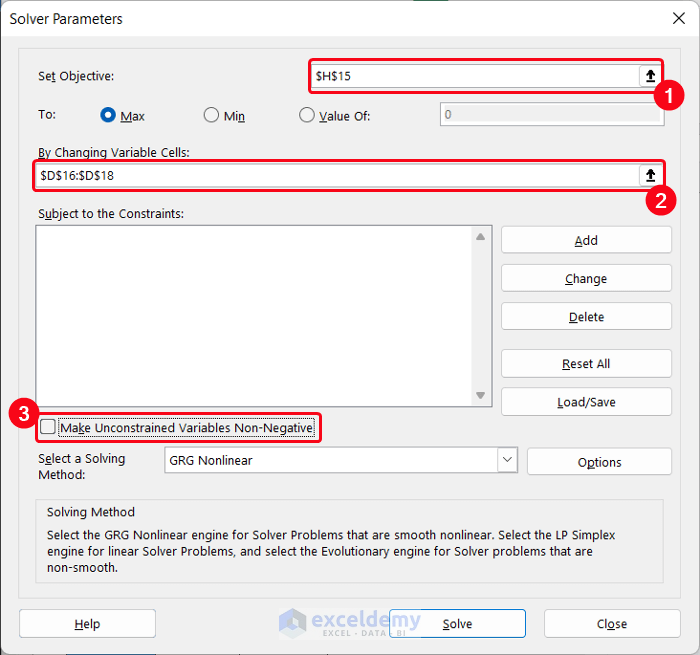
- A new dialog box named Solver Parameters will appear.
- In the Set Objective box, put the cell $H$15 either by selecting from the table or inputting the value (with the absolute reference).
- In the By Changing Variable Cells option, select the range of cells $D$16:$D$18.
- Uncheck Make Unconstrained Variables Non-Negative.
- Click the Solve button.
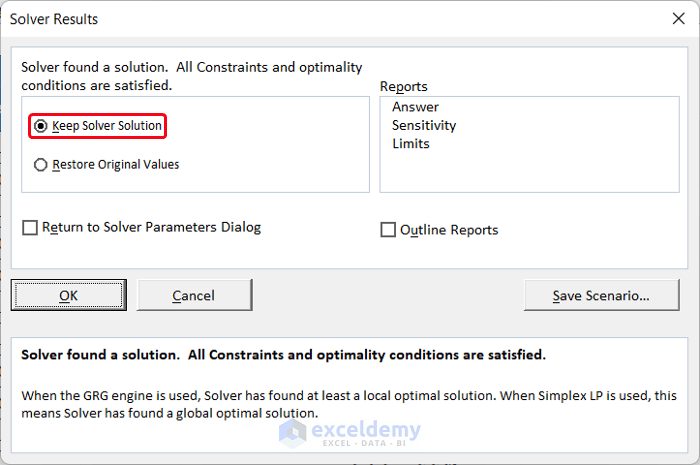
- The Solver Result box will appear in front of you.
- Choose the Keep Solver Solution. This box will also show you whether your regression analysis converged or diverged.
- Click OK to close the box.
- The variables in the range of cells D16:D18 have been changed. You will also see the values of columns E, F, G, and H are also changed.
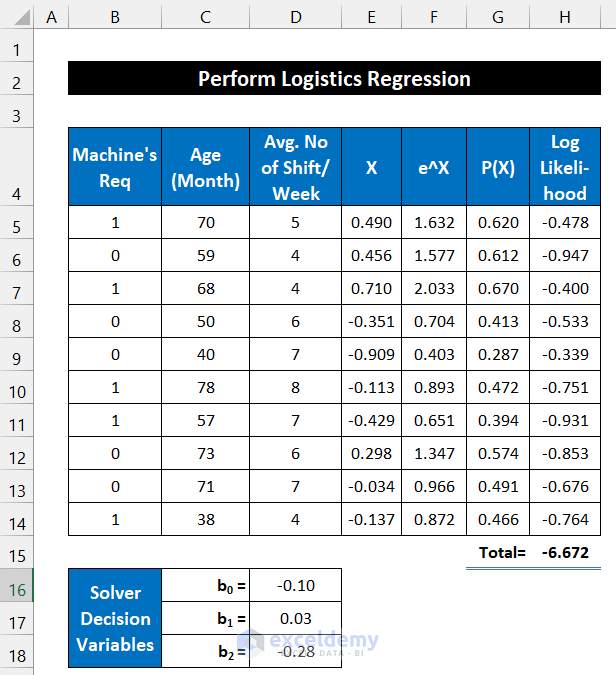
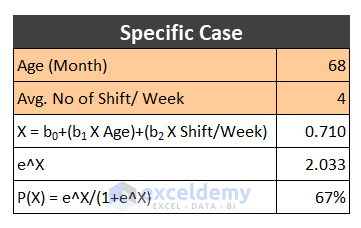
Illustration of a Binary Regression Analysis Result After the completion of the binary logistic regression analysis in Excel, you will see that our assumed regression variable value is substituted with the new analysis value and these values are the correct regression variable value of our dataset. We can consider the result of any specific data, like the machine which has an age of 68 months and works 4 shifts per week. The value of P(X) is 0.67. It illustrates to us that if we look for the machine in working condition the possibility of that event is about 67%. We can also show it separately, using the final values of the regression variable.
Read More: Multiple Linear Regression on Excel Data Sets
Download the Practice Workbook
Related Articles
- How to Do Multiple Regression Analysis in Excel
- How to Interpret Linear Regression Results in Excel
- How to Interpret Regression Results in Excel
- How to Interpret Multiple Regression Results in Excel
- How to Plot Least Squares Regression Line in Excel
- How to Do Simple Linear Regression in Excel
- How to Do Linear Regression in Excel
- How to Calculate P Value in Linear Regression in Excel
<< Go Back to Regression Analysis in Excel | Excel for Statistics | Learn Excel
Get FREE Advanced Excel Exercises with Solutions!


Hi! How do you assume what b0, b1 and b2 are? Are there always 3 or is it one for the dependent+1 for each indicator you are testing?
Dear Ella,
Thank you for your comment. I will try to provide a proper answer to your question.
The first answer is, to set the value for b0, b1, and b2, you can assume any values. Then, you can optimize the assumed values.
The answer to the second question is, since we have 2 independent and one dependent variable, we took 3 initial problem-solver variables. One for the dependent variable, and then for each independent variable, we took 1 additional problem solver variable.
I hope this will help you.
Regard,
Afia Aziz Kona
Thank you for this post. Very instructive.
What if I have more than 2 independent variables (5 to be specific), how do i use the Log-Likelihood formula, :
=(B5*LN(G5))+((1-B5)*LN(1-G5))
Does it remain as is or does it change based on the number of independent variables?
Hello SEUN OLALEYE,
Hope you are doing all well. Let’s get into your query first.
In this case, the Log-Likelihood formula doesn’t rely on the number of independent variables. In the case of 5 independent variables, the formula would be the same. The change will happen in the formula of the Logit value (X).
X = b0 + (b1 * ind var 1) + (b2 * ind var 2) + (b3 * ind var 3) + (b4 * ind var 4) + (b5 * ind var 5)The only change will happen here. All the remaining formulas will be the same.
For a better understanding, please go through the entire article again. Happy Excelling.
Regards,
SHAHRIAR ABRAR RAFID
Team ExcelDemy
Hello, Im having an issue. Sometimes after pressing the Solve button, it comes back with an error stating “one of the cells in the worksheet became an error value when Solver tried certain values for the Variable Cells”. When I go back to the worksheet, there is a #NUM! error in one or 2 cells in the Exponential Value column.
Any ideas as to why this is happening? Any help would be greatly appreciated.
Thanks, MIKE M for your question. The problem you are stating indicates that the Solver could not find a solution that satisfied the optimization constraints you specified. This can happen for several reasons, including Incorrect input data, Incorrect model specification, Insufficient or incorrect constraints, Numerical instability, etc. Try to rectify those issues or if you need a more specific solution to your problem, it would be convenient if you provide your dataset. Thanks for being with ExcelDemy.
Regards
Mohammad Shah Miran
Team ExcelDemy