[Fixed] QUADF Not Working in Excel

There is no built-in function in Excel for computing proper or improper integrals. However, we can use a dedicated add-in, ExceLab 365 Calculus Functions, from the Microsoft AppSource. The add-in provides a function named QUADF that can calculate the integrals. But unfortunately, the QUADF function doesn’t always work as expected.

In this article, we’ll discuss why the QUADF function may be returning errors, and present an alternative way to calculate the integrals in Excel if and when it does.

Reasons Why the QUADF Function Is Not Working in Excel and the Solution

There may be some issues with this add-in QUADF function. Sometimes it shows an error when it shouldn’t.

Possible Reasons Why QUADF Is Not Working in Excel

The possible reasons why the function may not be working are:

• The QUADF function is disabled in Excel. Install the ExceLab 365 Calculus Functions Add-in in your Excel application and it should then work.
• If you fail to define an initial value in he function, it will return a #NUM! Error.
• But sometimes you get a #VALUE! Error , which can be for several reasons, one of which is that the function is buggy in Excel 365.

To explain the problem, we have taken the following integral function to apply the QUADF function:

In this function, we set the lower limit 1 and the upper limit 4.

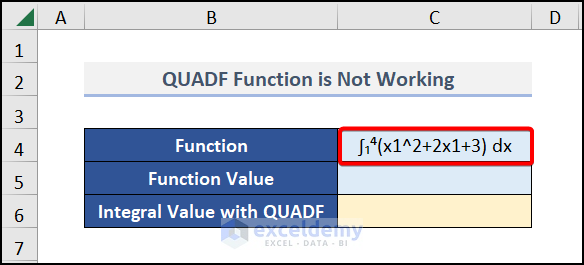
To calculate the integral, we need to calculate the function value with a random x1 value. For our case, we use 1 for the x1 value, and we get the function value 6 for that value.

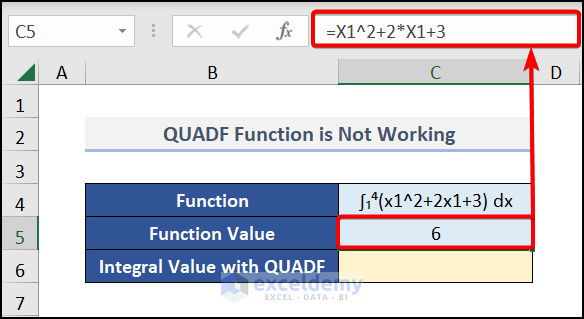
At this point, we use the QUADF function for computing the integrals. In cell C6 we enter the below formula:

Here, C5 is the function value f, and X1 is the value for which we have the function value. 1 is the lower limit and 4 is the upper limit.

Press ENTER.

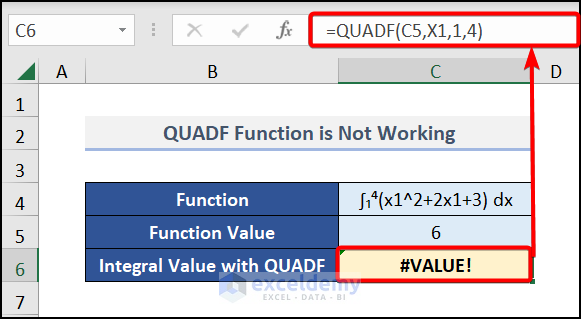
Oops! A #VALUE! Error is returned by the QUADF function.

A Suitable Solution Using the Mid Point Rule

From the above example, it is clear that the QUADF function is not working properly. Here is an alternative but effective solution to calculate the integrals, using the MidPoint Rule, also known as Simpson’s Rule. Conveniently, no add-ins are required to apply this method.

The value of the integral is 45 when we estimate it manually. Now, let’s try to show the same integral value using our method.

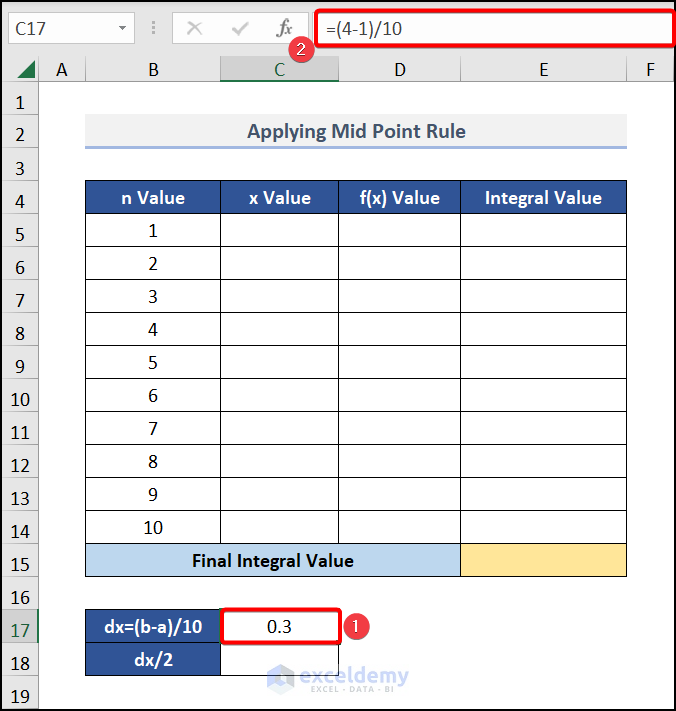
• In cell C17, enter the following formula:

Here, 4 and 1 represent the b and a values respectively, which are the upper bound and the lower bound of the integral. 10 is the number of steps (the n Value).

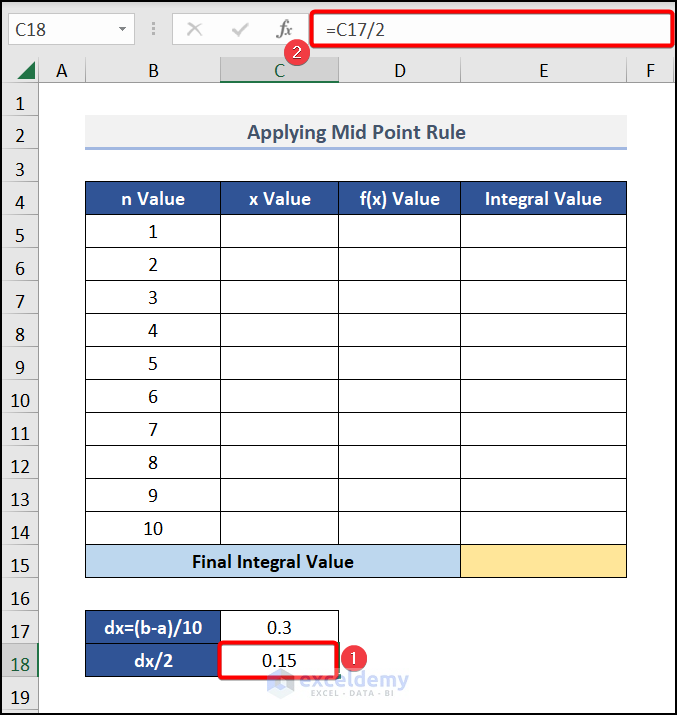
• Enter the formula given below in cell C18:

Here, cell C17 represents the value of dx.

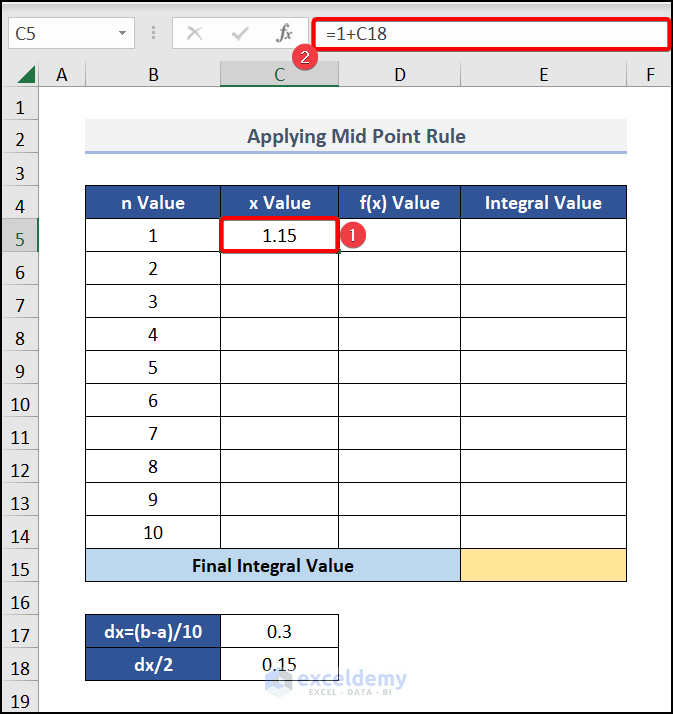
• Insert the following formula in cell C5:

Here, cell C18 indicates the value of dx/2.

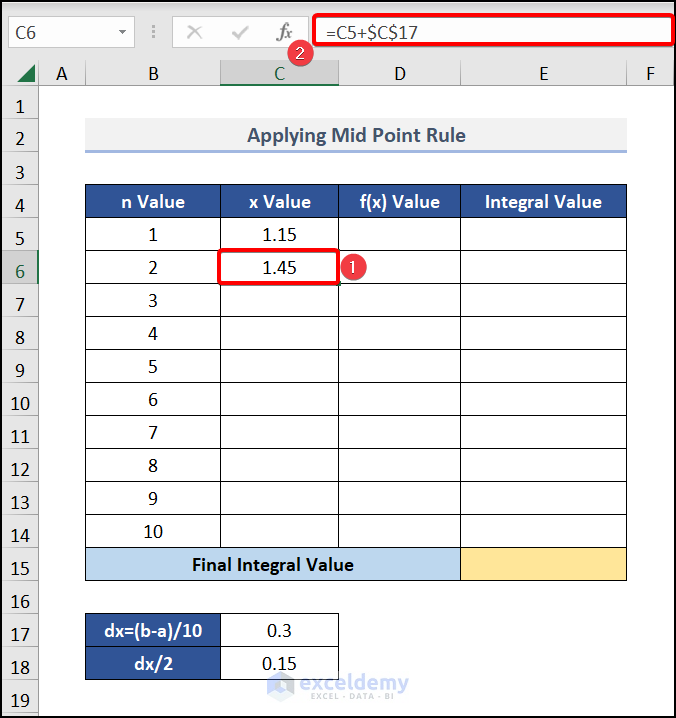
• In cell C6, insert the following formula:

As a result, wel have the x Value for the 2nd step.

• Press ENTER and drag down the Fill Handle tool to get the values for the other cells.

We have the following output for the x Value:

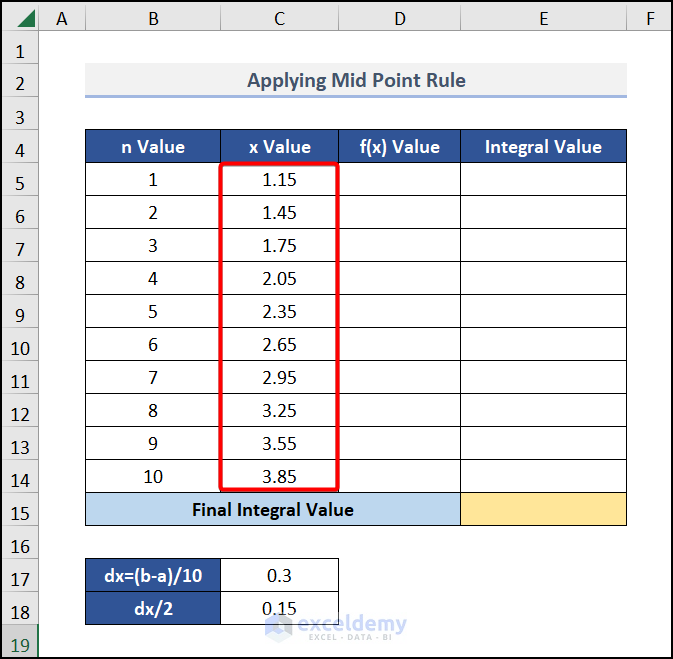
Now we will calculate the f(x) value.

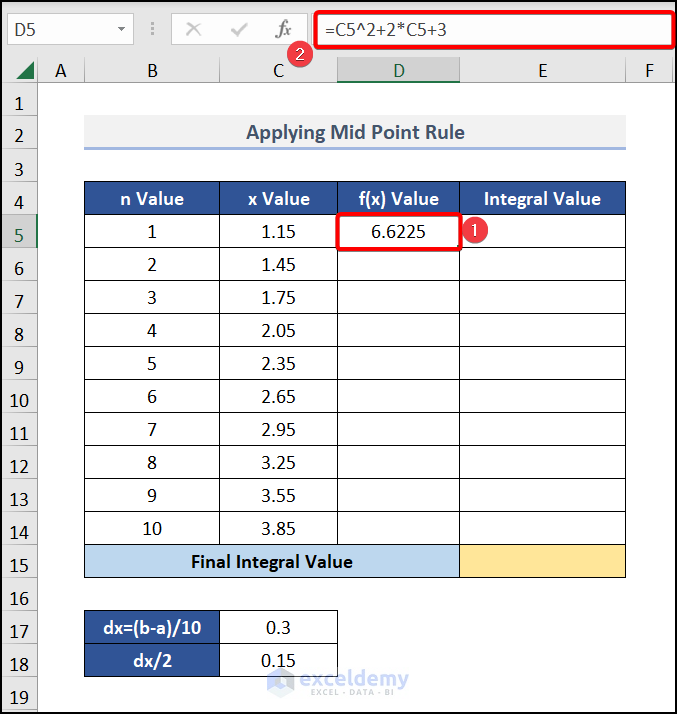
• In cell D5, enter the following formula:

Here, cell C5 refers to the x Value.

• Drag the formula down for the other cells to get the below output:

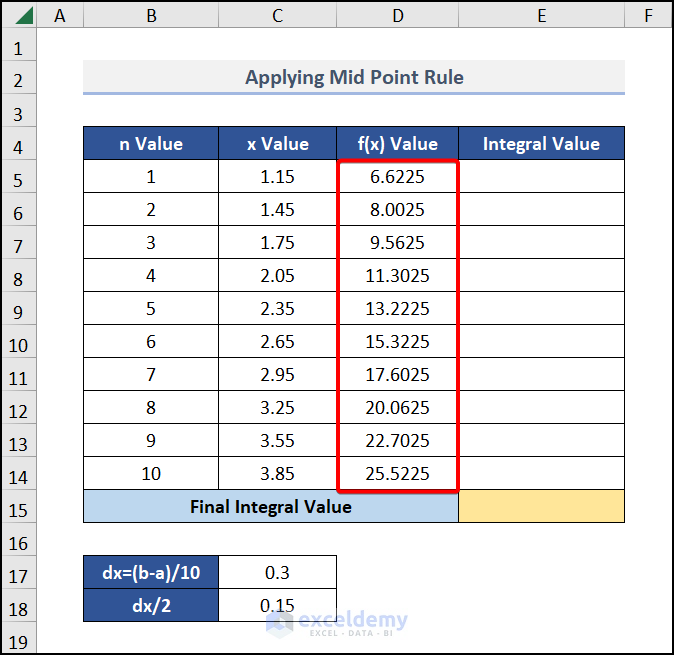
Now, we will calculate the individual integral values for each step.

• In cell E5, enter the following formula:

Here, cell D5 indicates the f(x) Value.

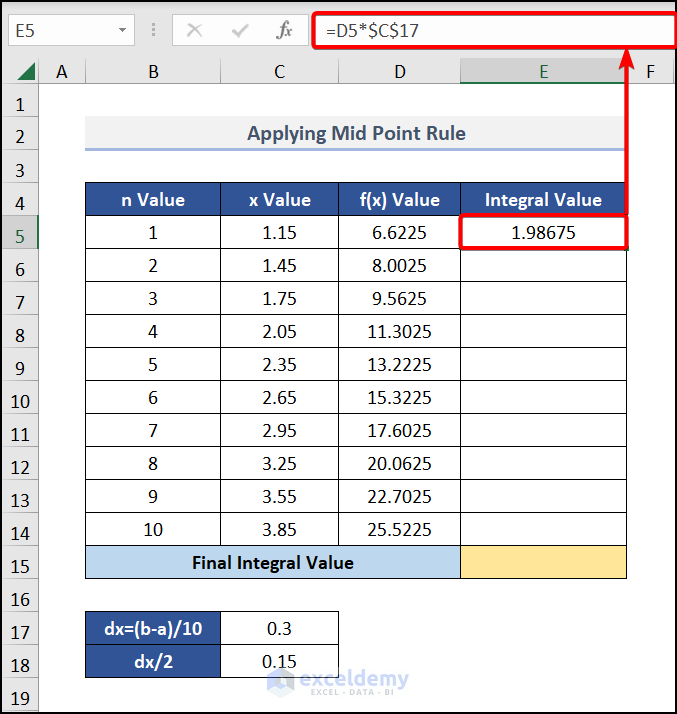
Press ENTER and drag the formula down to get the result below:

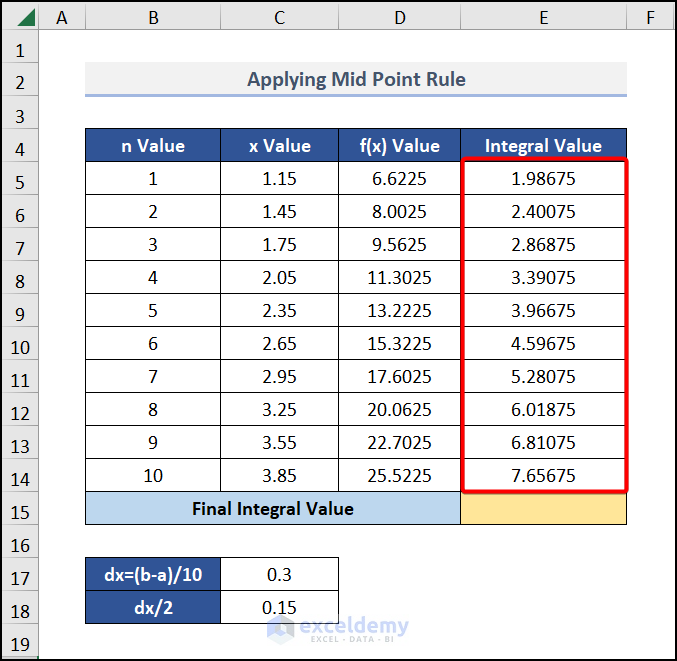
Lastly, we use the SUM function to evaluate the sum of the integral values.

• In cell E15, insert the following formula:

This will calculate the arithmetic sum of all 10 integral values.

• Press ENTER and drag the formula down to other cells.

The Final Integral Value of 44.9775 is so close to our desired result of 45.

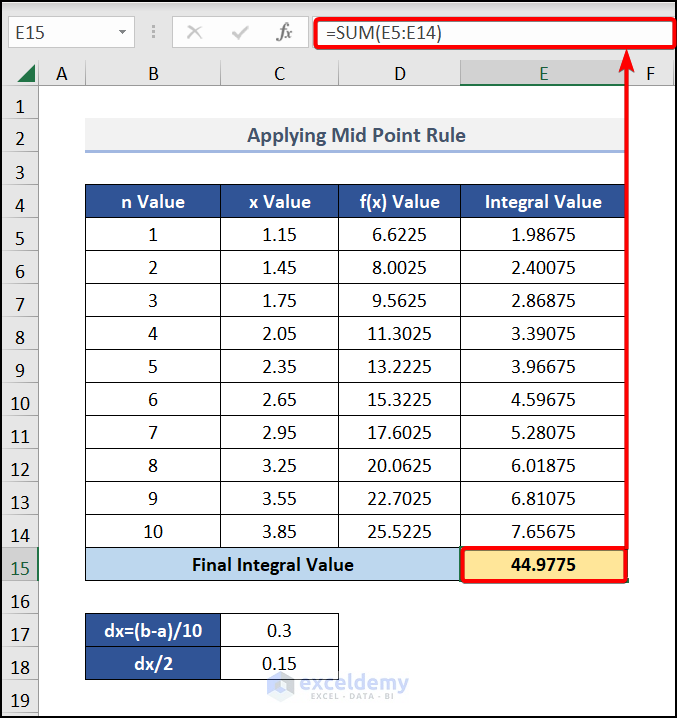
So, we can say that the Mid Point Rule is an effective workaround to the issue of QUADF not working.

Download Practice Workbook